Zaman Serileri Wooldridge 18. Bölüm

Bu bölümde ileriye yönelik zaman serisi tahminleri yöntemlerinden bahsedeceğiz

İleriye Yönelik Tahmin Etme?

Hepinizin bildiği gibi iktisat biliminin bazı dalarında ileriye yönelik tahmin çok önemli bir yer tutar.Biz şimdilik regresyona bağlı bir tahmin yöntemi kullanacağız. Bu bölümde kullanacağımız örnekler Wooldridge ders kitabınızda bulunan örneklerden oluşacak. Bir veri setinin t zamanına kadar değerlerini bildiğimizi varsayalım. Bu zaman serisinin t+1 zamanında nasıl bir değer alacağını tahmin etmek ileriye yönelik tahmin etme olarak adlandırılır. Bu t+1 zamanının tahmini, veri setimizin yapısına göre değişkenlik gösterir. Eğer bir hisse senedi veya döviz kuru tahmini yapıyorsak, bu sürec bir günlük tahmin olabilir. Eğer GSYH’yı tahmin etmek istiyorsak, 3 ay veya 1 yıl sonrayı tahmin etmeye çalışabilirsiniz. Bazı veri setleri aylık verilerden oluşur ve bir ay sonrayı tahmin etmek isteyebilirsiniz.

Peki elde ettiğimiz tahminin, iyi bir thamin olup olmadığını nasıl anlayabiliriz. Wooldridge, yapmış olduğumuz tahmine $f$ (forecast) notasyonunu kullanmış. Eğer tahmin etmeye çalıştığımız $y_{t+1}$, $f$ değerinden farklı oluşursa. Tahminimiz bir hata payına sahip olur. İleriye yönelik tahmin hatası dediğimiz bu hataya $e$ diyelim. O zaman hata

$$ e_{t+1} = y_{t+1} - f_t $$

olacaktır. $f_{t}$, $y_{t+1}$ için t zamanında yapmış olduğumuz tahmindir. $y_{t+1}$ ancak tahmin yapıldıktan sonra gözlemlenebilir ve biz hatamızın ne kadar olduğunu anlayabiliriz. Tahmin edebileceğiniz gibi hata payları negatif ve pozitif olacağından, toplam hata payı kareler alınarak bulunur. Bu yöntemi daha önce regresyon ve varyans için de kullanmıştık. $e_{t+1}^2$

Kullanılan Regresyon Modelleri

Tahmin etmek istediğimi bir y değişkeni olduğunu varsayalım. Regresyon modelimiz

$$ y_t = \beta_0 + \beta_1 z_t + u_t $$

Bu regresyon modelini tahmin ederek $\beta_0$ ve $\beta_1$ parametrelerini tahmin edebiliriz ve aynı denklemi bir adım ilerisi için yazarsak

$$ y_{t+1} = \beta_0 + \beta_1 z_{t+1} + u_t $$

eğer $z_{t+1}$' ı biliyorsak $y_{t+1}$‘ı tahmin edebiliriz. Ancak bir zaman serisinde geleceğe yönelik veriler çoğunlukla bilinemez.

eğer $z_{t+1}$‘ı bilmiyorsak veya tahmin edemiyorsak şu şekilde bir denklem yazmamız daha yararlı olacaktır.

$$ y_t = \beta_0 + \beta_1 y_{t-1} + \beta_2 z_{t-1} + u_t $$ Bu tür modellerde, tahmin için z değişkeni kaldırılabilir veya daha fazla gecikme değerleri alınabilir.

Wooldridge Tahmin

library(wooldridge)
library(stargazer)

## 
## Please cite as:

##  Hlavac, Marek (2018). stargazer: Well-Formatted Regression and Summary Statistics Tables.

##  R package version 5.2.2. https://CRAN.R-project.org/package=stargazer

library(rmarkdown)
library(dynlm)

## Loading required package: zoo

## 
## Attaching package: 'zoo'

## The following objects are masked from 'package:base':
## 
##     as.Date, as.Date.numeric

data(phillips, package = "wooldridge")
paged_table(phillips)

tsph<-ts(phillips, start = 1948)
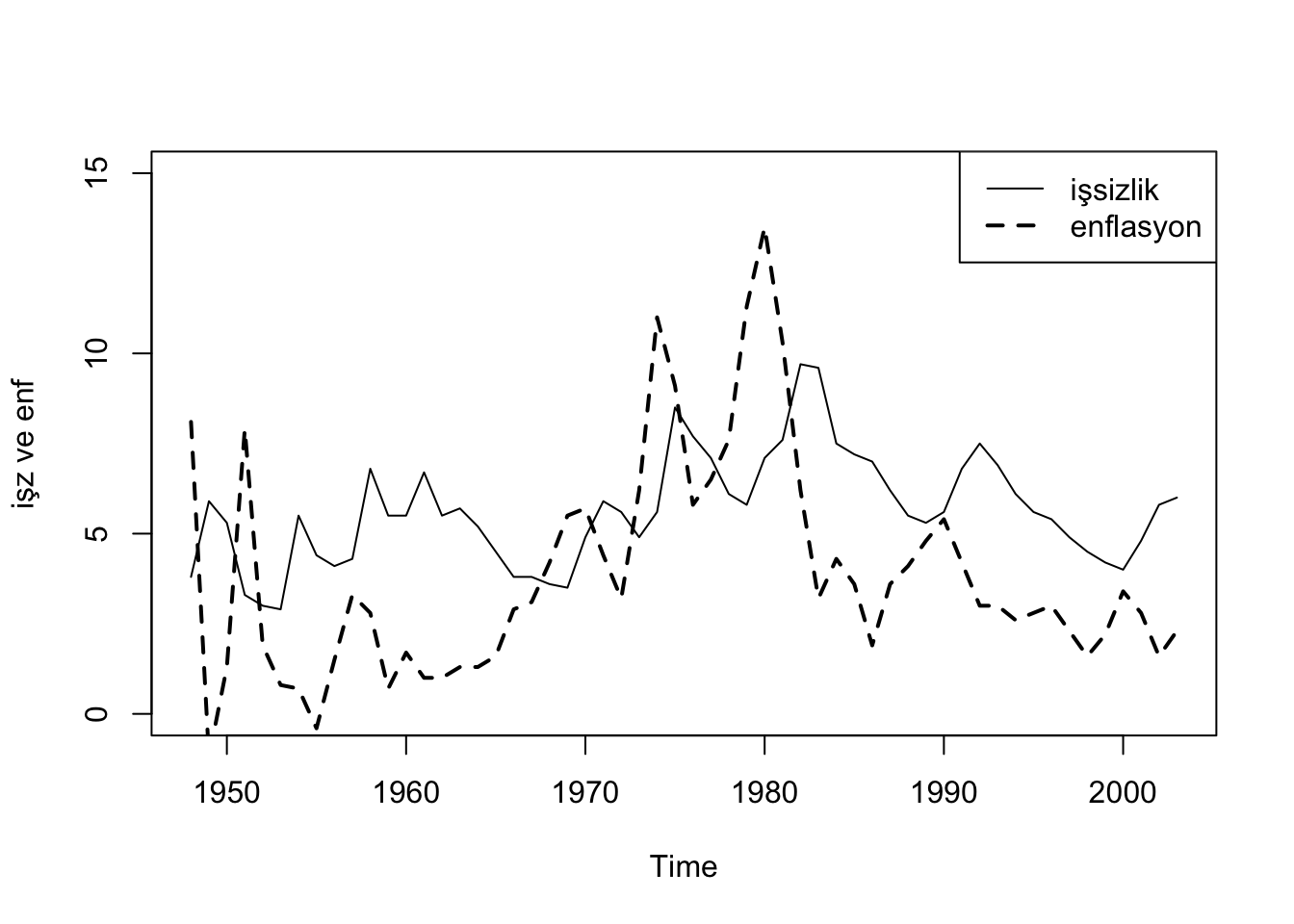
plot(tsph[,"unem"],lty=1, lwd=1, ylim=c(0,15), ylab=("işz ve enf"))
lines(tsph[,"inf"],lty=2, lwd=2)
legend("topright", c("işsizlik","enflasyon"), lty=c(1,2), lwd = c(1,2))

model1<-dynlm(unem~L(unem),data=tsph, end=1996)
model2<-dynlm(unem~L(unem) + L(inf),data=tsph, end=1996)

stargazer(model1,model2,type ="text" )

## 
## =================================================================
##                                  Dependent variable:             
##                     ---------------------------------------------
##                                         unem                     
##                              (1)                    (2)          
## -----------------------------------------------------------------
## L(unem)                    0.732***               0.647***       
##                            (0.097)                (0.084)        
##                                                                  
## L(inf)                                            0.184***       
##                                                   (0.041)        
##                                                                  
## Constant                   1.572***               1.304**        
##                            (0.577)                (0.490)        
##                                                                  
## -----------------------------------------------------------------
## Observations                  48                     48          
## R2                          0.554                  0.691         
## Adjusted R2                 0.544                  0.677         
## Residual Std. Error    1.049 (df = 46)        0.883 (df = 45)    
## F Statistic         57.132*** (df = 1; 46) 50.219*** (df = 2; 45)
## =================================================================
## Note:                                 *p<0.1; **p<0.05; ***p<0.01

f1<-predict(model1,newdata = window(tsph,start=1997))

f2<-predict(model2,newdata = window(tsph,start=1997))

y<-window(tsph,start=1997)[,"unem"]

time=c(1997:2003)
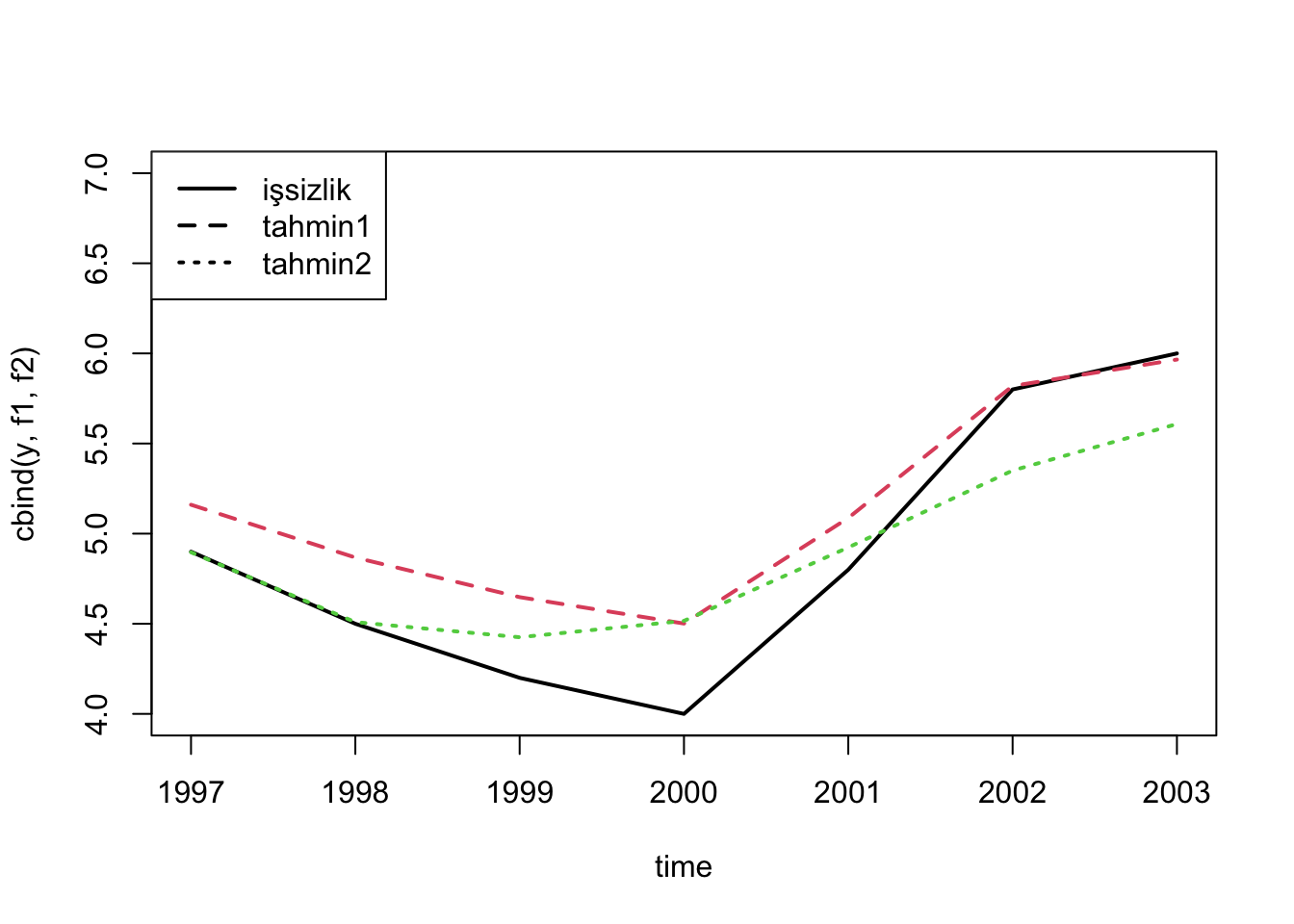
matplot(time,cbind(y,f1,f2),type = "l",lwd=2,lty=1:3, ylim = c(4,7))
legend("topleft", c("işsizlik","tahmin1","tahmin2"),lwd=2,lty = 1:3)

e1<-y-f1
e2<-y-f2
rmse<-sqrt(mean(e1^2))
mae<-mean(abs(e1))
<<<<<<< HEAD

rmse2<-sqrt(mean(e2^2))
mae2<-mean(abs(e2))

=======
>>>>>>> origin
rmse

## [1] 0.3247281

mae

## [1] 0.2738516

<<<<<<< HEAD
=======
rmse2<-sqrt(mean(e2^2))
mae2<-mean(abs(e2))
>>>>>>> origin
rmse2

## [1] 0.3135421

mae2

## [1] 0.2455728

«««< HEAD

=======

origin