Durağan (Stationary) Zaman Serileri
Zaman serisi regresyonlarında, bildiğiniz doğrusal regresyon varsayımlarının yanında bit varsayıma daha ihtiyaç duyarız. Bu varsayım, durağanlık (stationarity) varsayımıdır.
Durağanlık varsayımına göre, regresyon hata payı $u$‘nun dağımı ve $u$‘nun terimlerinin zaman içindeki korelasyonları zamana göre değişmez. Hata payının ortalamasının ve varyansının zaman değiştikçe sabit olmasını bekleriz.
Bu terimleri konuşmaya bir örnekle başlayalım. Bu örneğimizde Türkiye için Phillips Eğrisini tahmin edeceğiz.
Verileri indir
WDI data setinden Türkiye için işsizlik ve enflasyon verilerini elde edeceğiz. WDI paketini R’a çağırın. https://data.worldbank.org/indicator internet sitesinden işsizlik ve enflayon kodlarını bulun ve R’a yükleyin. İşsizlik Education sekmesinin altında, Unemployment, total ismiyle bulabilirsiniz ve kodu SL.UEM.TOTL.ZS olarak göreceksiniz. Enflasyon verisi Economy and Growth başlığının altında, Inflation, consumer prices adıyla bulabilirsiniz ve kodu FP.CPI.TOTL.ZG olarak göreceksiniz.
library(WDI)
df = WDI(indicator=c(un='SL.UEM.TOTL.ZS', enf='FP.CPI.TOTL.ZG' ), country=c('TR'), start=1992, end=2020)
df isimli bir veri seti hazırladık. İsimler karışık olduğu için rahatça anlayabileceğimiz un ve enf isimlerini verdik. Türkiye verilerini indirmek için TR kodunu kullandık. 1992 ve 2020 arası verileri indirdik.
Veri setini zaman serisi (time series) olarak kaydetmemiz gerekir. ts() fonksiyonu bize yardımcı olacaktır.
library(dynlm)
## Loading required package: zoo
## Attaching package: 'zoo'
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric
df.ts <- ts(df, start=c(1992), end=c(2020),frequency=1)
Veri setimizin içinde kullanmıyacağız değişkenler var. Mesela TR veya Turkey her zaman dilimi için aynı olacaktır. Çünkü sadece Türkiye verisini indirdik. Zaman serisine çevirdiğimiz için year verisine de ihtiyacımız yok.
df.ts<-df.ts[,c("un","enf")]
Kareli parantez veri setinin içindeki satırları ve sütunları seçmemize yarar. Virgülden önce hangi satırları istediğimizi, virgülden sonra hangi sütunları istediğimizi yazabiliriz. Bütün satırları istiyoruz ve sadece un ve enf değişkenlerine ihtiyacımız var. Bu yüzden df.ts veri setimizi sadece bu iki değişkenden oluşturduk.
Şimdi bu iki değişkenin grafiklerini çizelim.
plot(df.ts[,"un"], ylab="işsizlik")
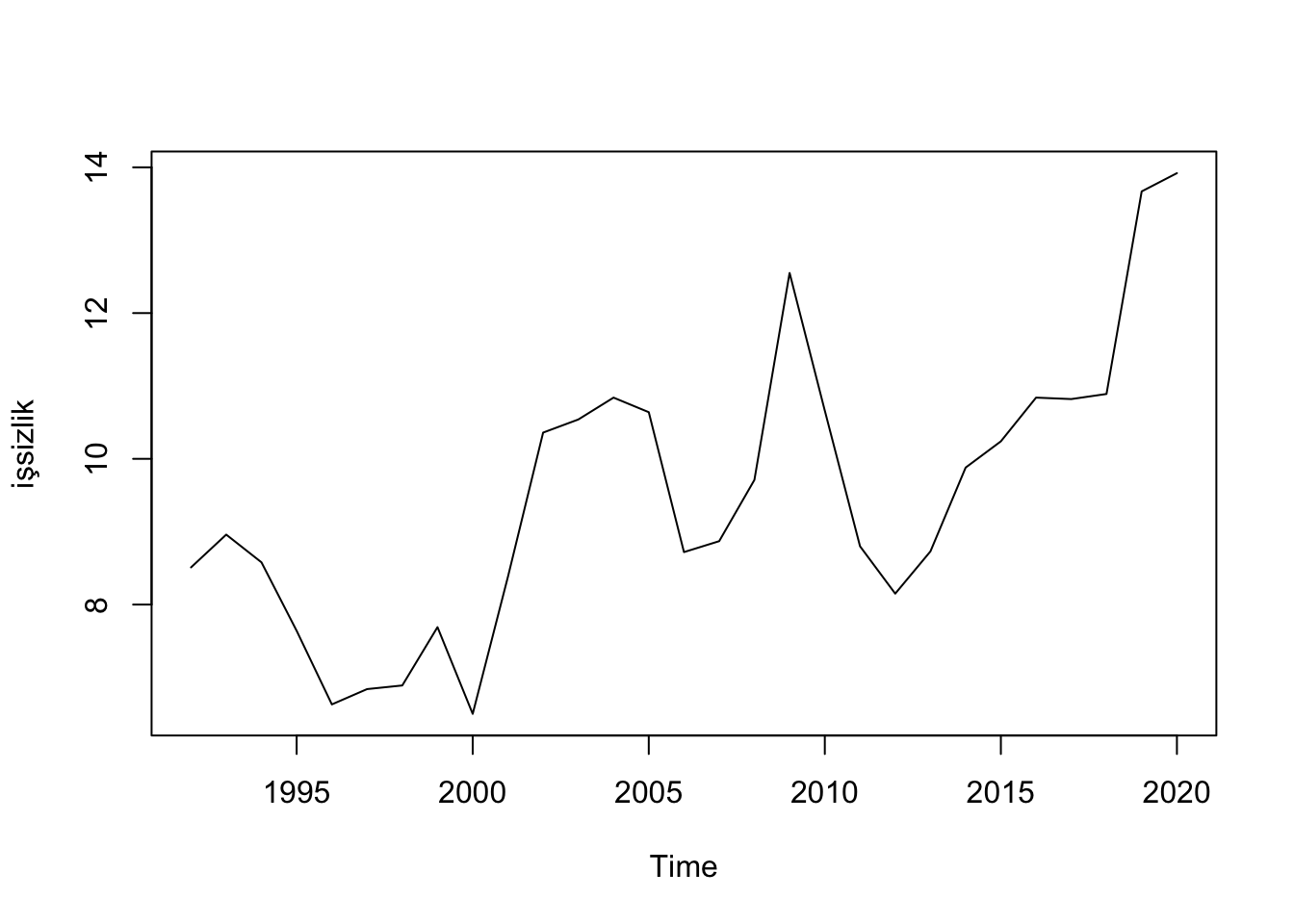
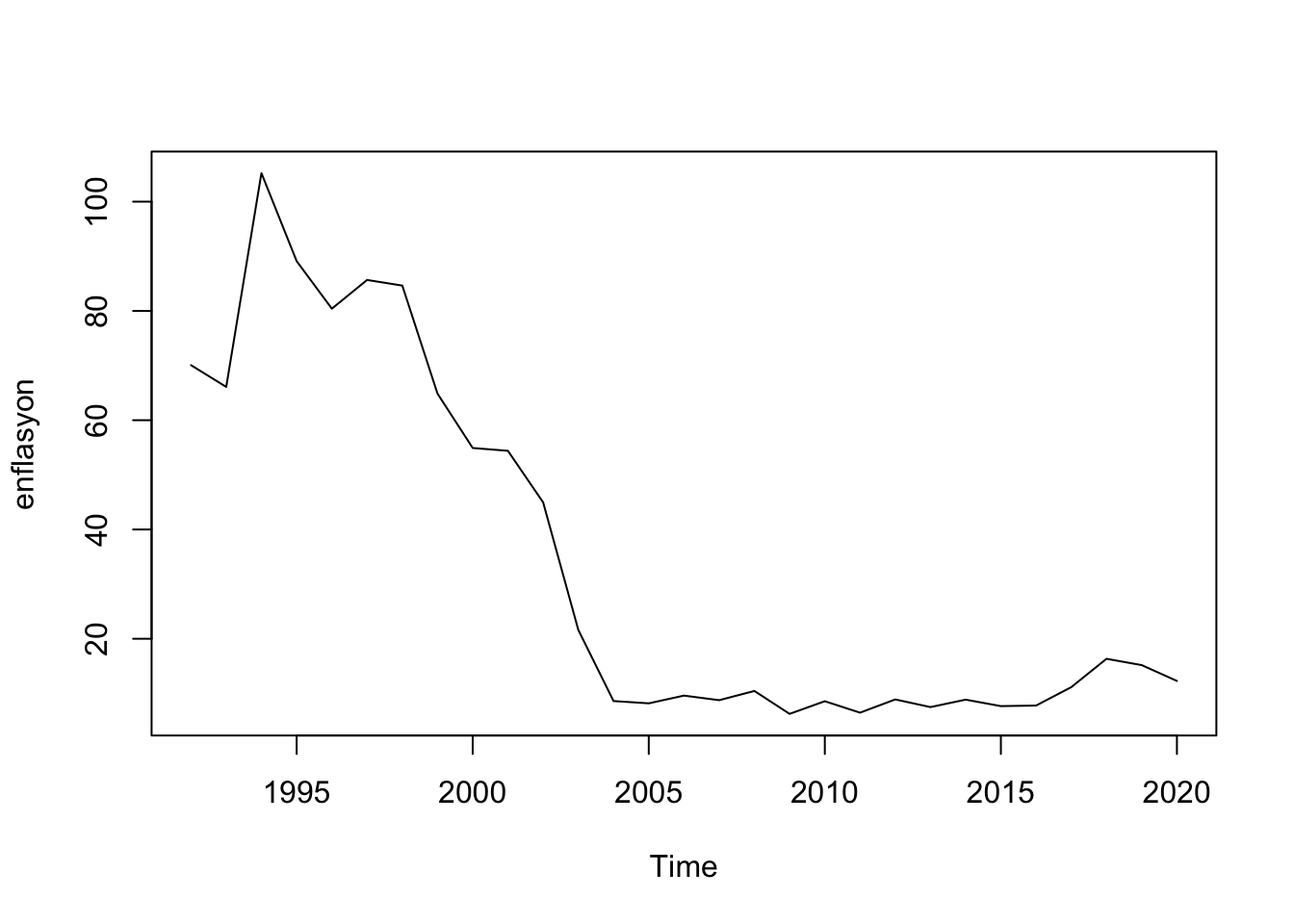
plot(df.ts[,"enf"], ylab="enflasyon")
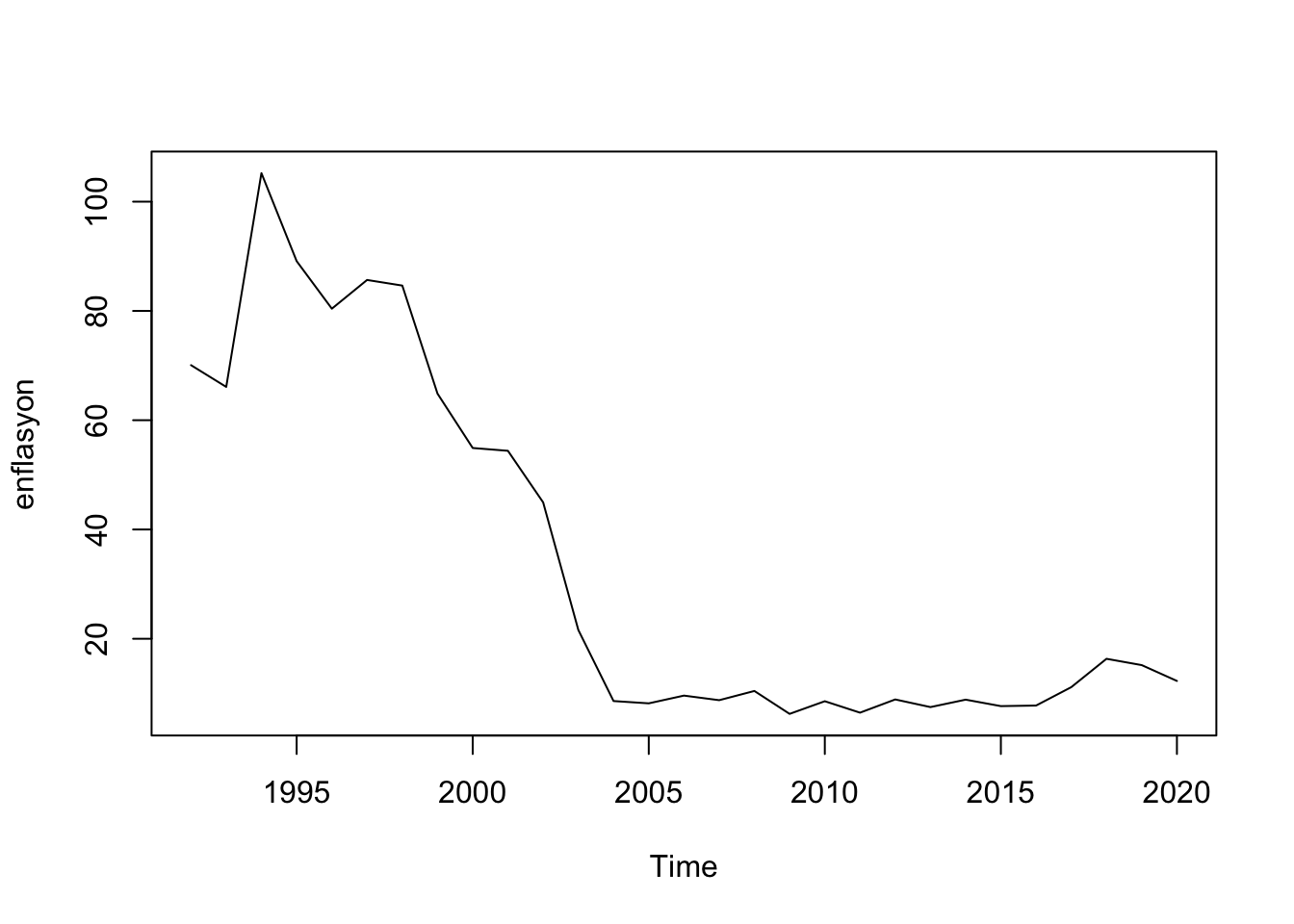
Her bir zaman serisi değişkeninin kendisinin bir zaman öncesiyle koralasyonunun olup olmadığını incelememiz gerek. Bu koralasyona otokorelasyon denilir. Oto kendi kendiyle korelasyonu anlamına gelir. Her bir seri için bir gecikmeli zaman serisi yaratıp otokoralasyonlarına bakalım.
gecikmeliun <- data.frame(cbind(df.ts[,"un"], lag(df.ts[,"un"],-1)))
names(gecikmeliun) <- c("un","un1gec")
head(gecikmeliun)
## un un1gec
## 1 8.51 NA
## 2 8.96 8.51
## 3 8.58 8.96
## 4 7.64 8.58
## 5 6.63 7.64
## 6 6.84 6.63
unbirgec, un verisinin bir gecikmeli halidir. Atokoralasyon için acf fonksiyonu, serinin bütün gecikmeleri için korelasyon grafiği oluşturur. Bir serinin kendisiyle korelasyonu tahmin edebileceğiniz gibi 1 dir.
acf(df.ts[,"un"])
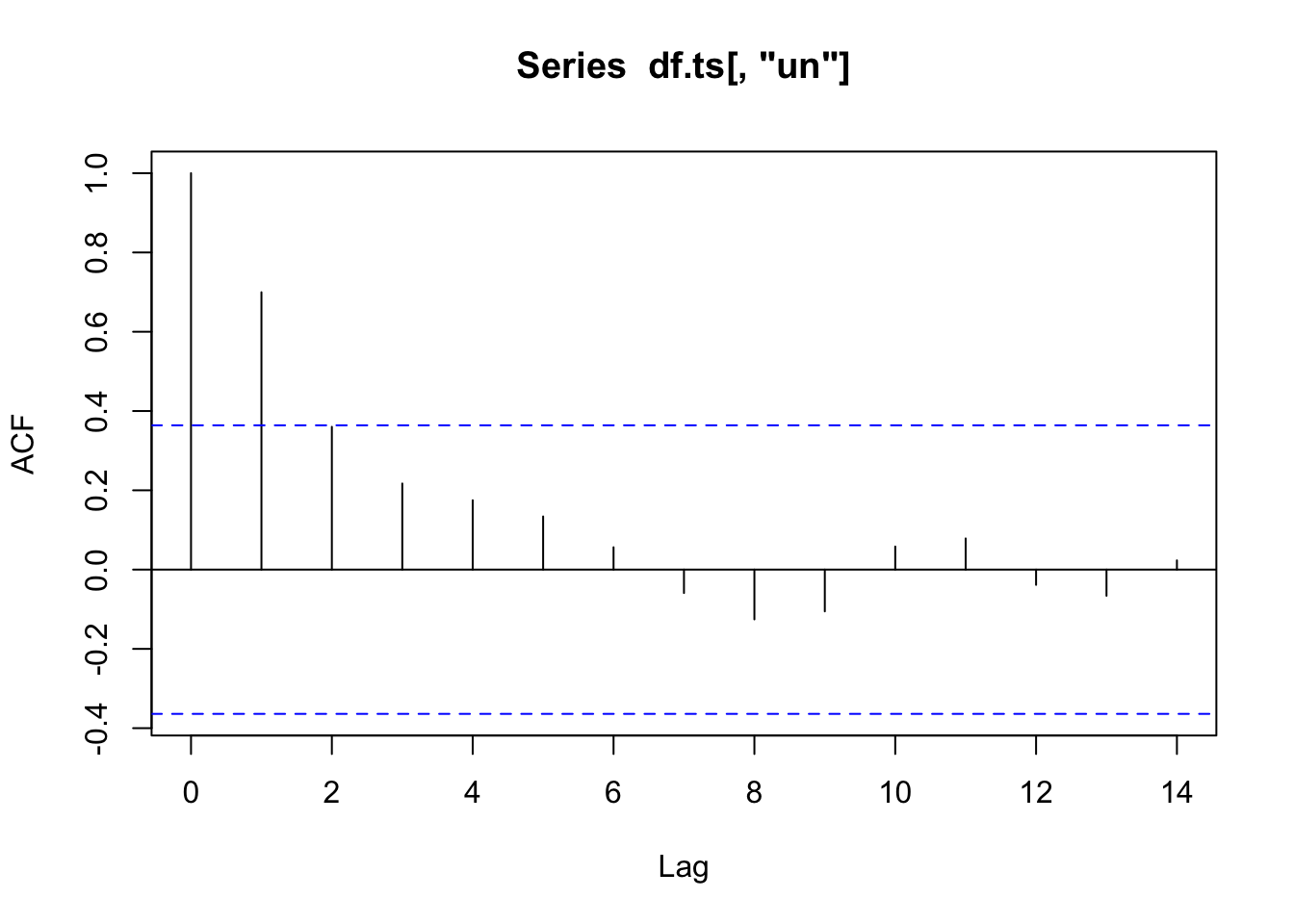 0 serinin kendisiyle olan korelasyonunu gösterir. O yüzden grafik hep birden başlar. -0.4 ve 0.4 arası serilerin arasında korelasyon olmayadğını gösteren uç noktalardır ve mavi kesikli çizgiyle gösterilir. Anlıyoruz ki işsizlik sadece bir gecikme ile otokorelasyonludur.
0 serinin kendisiyle olan korelasyonunu gösterir. O yüzden grafik hep birden başlar. -0.4 ve 0.4 arası serilerin arasında korelasyon olmayadğını gösteren uç noktalardır ve mavi kesikli çizgiyle gösterilir. Anlıyoruz ki işsizlik sadece bir gecikme ile otokorelasyonludur.
acf(df.ts[,"enf"])
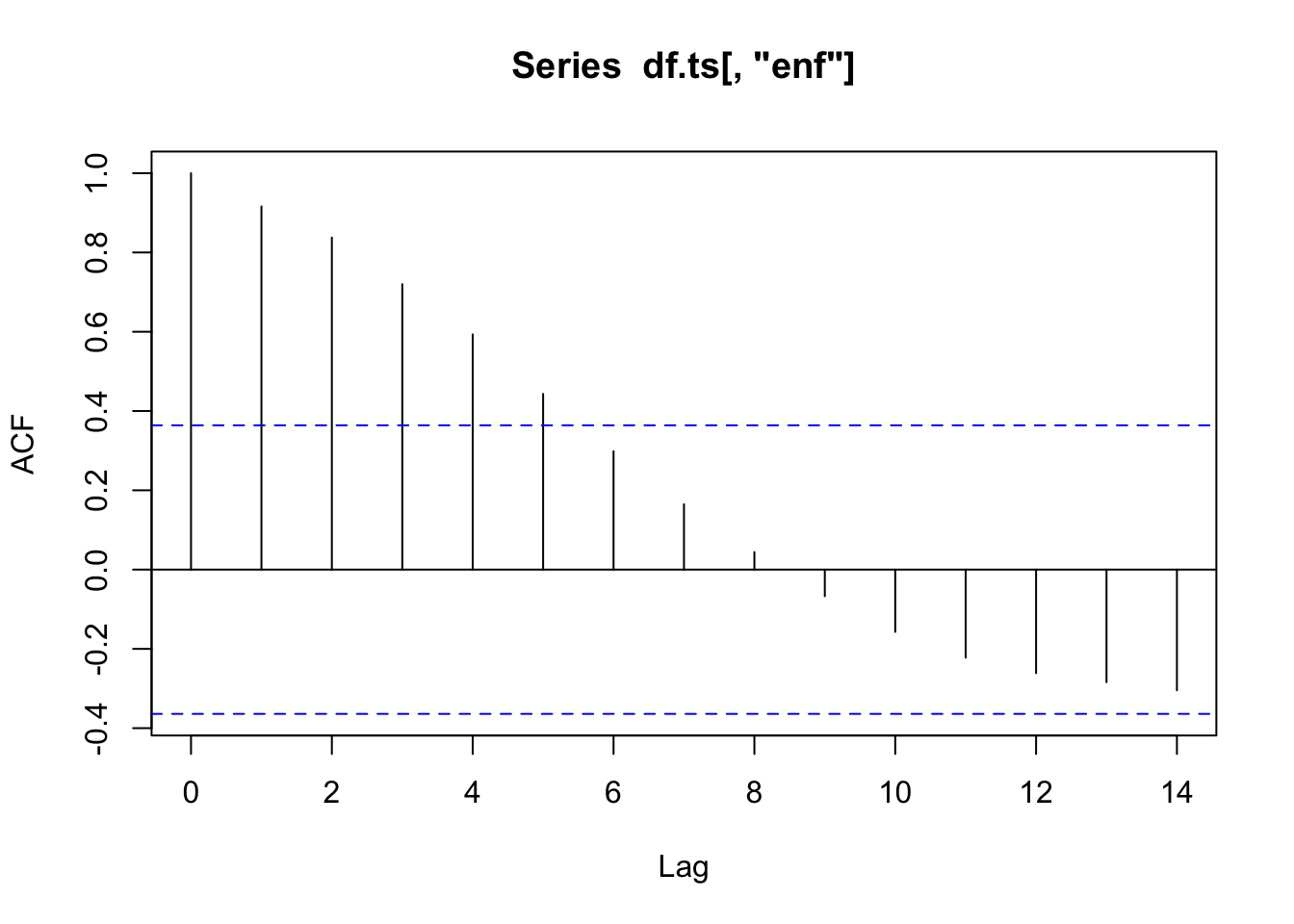
Enflasyon ise 5’ci gecikmeye kadar pozitif otokorelasyon gösterir. işsizliğin ilk farkı alınmış serisini yaratalım ve Phillips eğrisi regresyonunu yapalım.
$$ inf = \beta_0 + \beta_1 \Delta un + u $$
enflasyon <- df.ts[,"enf"]
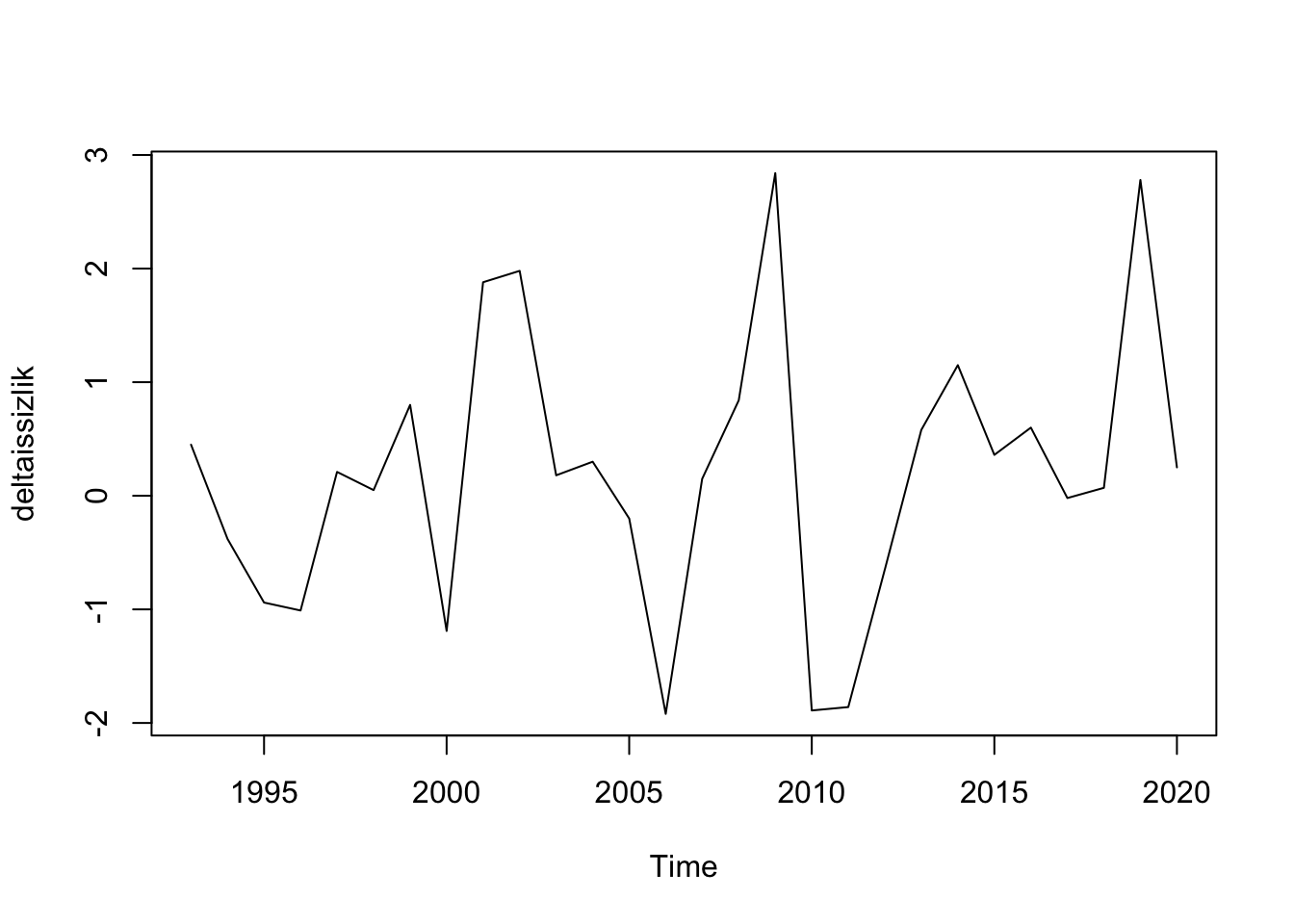
deltaissizlik <- diff(df.ts[,"un"])
plot(enflasyon)
plot(deltaissizlik)
phillips.reg <- dynlm(enflasyon~deltaissizlik)
summary(phillips.reg)
##
## Time series regression with "ts" data:
## Start = 1993, End = 2020
##
## Call:
## dynlm(formula = enflasyon ~ deltaissizlik)
##
## Residuals:
## Min 1Q Median 3Q Max
## -31.39 -24.05 -19.96 27.95 71.11
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 33.146 6.345 5.224 1.86e-05 ***
## deltaissizlik -2.535 5.190 -0.488 0.629
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 33.15 on 26 degrees of freedom
## Multiple R-squared: 0.009095, Adjusted R-squared: -0.02902
## F-statistic: 0.2386 on 1 and 26 DF, p-value: 0.6293
Regresyonu artık lm (linear model, doğrusal model) regresyonu ile yapmıyoruz. Zaman serisi kullandığımız için dynlm (dinamik lm) ile yapıyoruz. Aslında bu daha önce kullandığımız lm fonksiyonundan farklı değil. Ancak oluşturduğumuz yeni verilerde fark ve gecikme aldığımız için mevcut olmaya (not available, NA) değerler var. Bu yüzden bu fonksiyonu kullanmak daha doğru olacaktır.
Hata payına bir göz atalım.
uhat <- resid(phillips.reg)
plot(uhat)
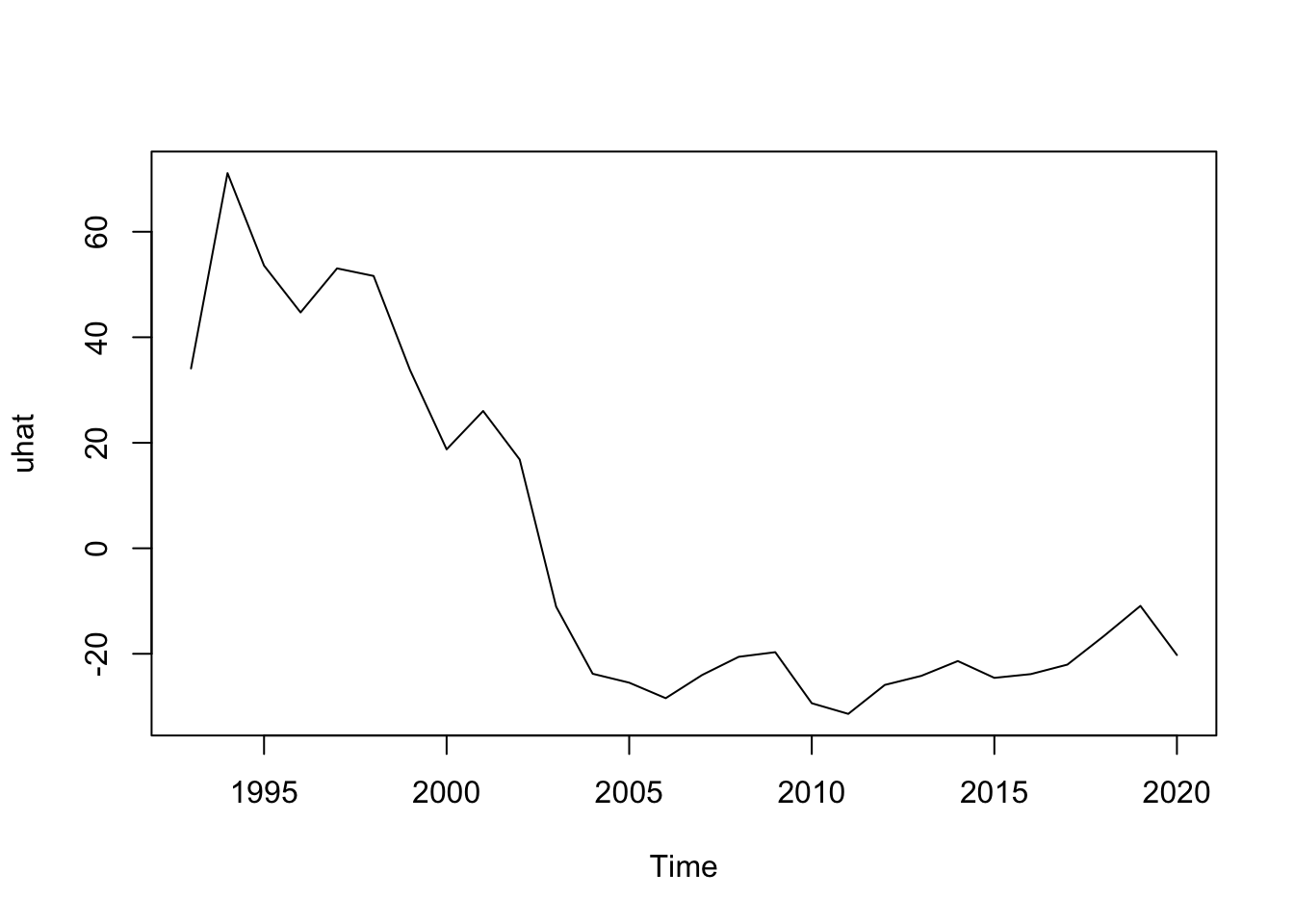
Hata payının zamana göre değişiklik gösterdiğini görüyoruz. Bu durum hata payı sabit ortalama değere sahip olmalı varsayımımıza aykırı. Bu yüzden anlamlılık düzeyini ölçmek için bulunan hata payları da yanlış.
Hata payının otokorelasyonunu da ölçelim.
acf(uhat)
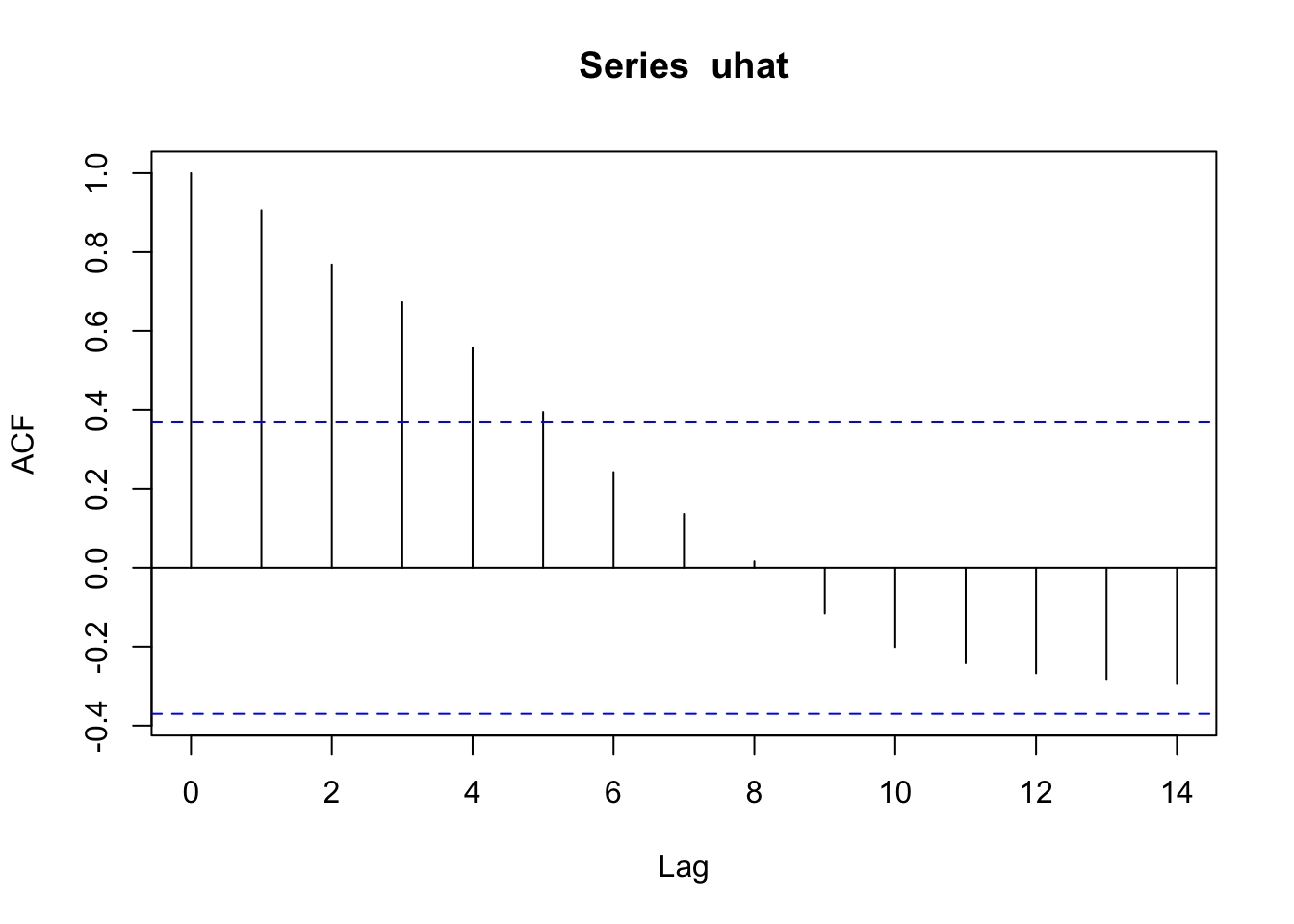
Hata payı beşinci gecikmesine kadar otokorelasyona sahip. Atokorelasyonu ölçmek için kullandığımız testlerden biri Breusch-Godfrey testidir.
Örneğimizi ele alalım.
$$ inf = \beta_0 + \beta_1 \Delta un + u $$
Hata payı u’nun otokorelasyona sahip olduğunu düşünüyoruz. Yani hata payının gecikmeli haliyle korelasyonu varsa, gecikmeli halinin önündeki katsayılar anlamlı ve sıfırdan farklı olmalı.
$$ u_t = \alpha_0 + \alpha_1 u_{t-1} + \epsilon $$
Bu durumda eğer $\alpha_1$ sıfıra eşit değilse. $u_t$ ve $u_{t-1}$ arasında korelasyon mevcuttur diyebiliriz.
Bu yüzde hipotez
$$ H_0: \alpha_1 = 0 $$ olur.
Eğer daha çoklu geciklemeri test etmek istersek F testi veya Chi kare istatitiğini kullanabiliriz. R’da Breusch-Godfrey testi şu şekilde yapılabilir.
library(lmtest)
bgtest(phillips.reg, order=1, type="F")
##
## Breusch-Godfrey test for serial correlation of order up to 1
##
## data: phillips.reg
## LM test = 128.37, df1 = 1, df2 = 25, p-value = 2.436e-11
library(lmtest)
bgtest(phillips.reg, order=1, type="Chisq")
##
## Breusch-Godfrey test for serial correlation of order up to 1
##
## data: phillips.reg
## LM test = 23.436, df = 1, p-value = 1.292e-06
Bu iki testte de olaılık değerlerinin (p-value) çok küçük olduğunu görüyoruz. Bu hipotezimizin doğru olma ihtimalinin çok düşük olduğunu gösteriyor. Dolayısıyla otokorelasyonu yoktur hipotezini tamin ettiğimiz reddediyoruz.
Otokorelasyon mevcut olduğu için, regresyonun gerçek anlamlılık düzeylerini bulmak için başka bir hata payı değeri kullanmalıyız. Bunun için heteroskadastisite ve otokorelasyon düzelten (heteroskedasticity and autocorrelation consistent, HAC) standart hatalar kullanacağız. Bu aynı zamanda Newey-West hata payı olarak bilinir.
library(sandwich)
coeftest(phillips.reg, vcov.=vcovHAC(phillips.reg))
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 33.1462 10.6321 3.1176 0.004416 **
## deltaissizlik -2.5353 5.1520 -0.4921 0.626780
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
coeftest(phillips.reg, vcov.=NeweyWest(phillips.reg))
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 33.1462 27.4021 1.2096 0.2373
## deltaissizlik -2.5353 9.5217 -0.2663 0.7921
coeftest(phillips.reg, vcov.=kernHAC(phillips.reg))
##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 33.1462 30.1010 1.1012 0.2809
## deltaissizlik -2.5353 9.4147 -0.2693 0.7898
Farklı varyans kovaryans matriksleri kullanıldığında, katsayıların değişmediğini, sadece standart hataların değiştiğini gözlemleyebilirsiniz. Bu katsayıların anlamlılık düzeyine etki eder.