Durağan Olmayan (Nonstationary) Zaman Serileri
Basitçe bir zaman serisinin ortalaması, varyansı ve zamana göre kovaryansı zaman içinde değişiklik gösteriyorsa, o zaman serisi durağan değildir diyebiliriz.
Durağanlık varsayımına göre, regresyon hata payı $u$‘nun dağımı ve $u$‘nun terimlerinin zaman içindeki korelasyonları zamana göre değişmez. Hata payının ortalamasının ve varyansının zaman değiştikçe sabit olmasını bekleriz.
Durağan olmayan serileri regresyona genellikle koyamayız. Durağan olmayan seriler, hatalı bir korelasyona sahip olabilirler ve analizimizi yanıltırlar. Bu duruma sahte (spurious) regresyon denilir. Zamanın değişimiyle birlikte hareket ediyormuş gibi görünen serilerin genellikle birbirleriyle bir ilgisi olmayabilir.
Bir regresyonda durağan olmayan serilerinin kullanılabilmesinin yolu eşbütünleşmedir (cointegration). Bu konuya daha sonra döneceğiz.
Eğer durağan olmayan serileri hatalı bir regresyon yapıp bir araya getirmek istemiyorsak, zaman serilerinin durağan olup olmadığını test etmeliyiz. Eğer durağan değil ise bu zaman serilerini önce durağan hale getirmeliyiz.
Örnek veri seti indirme
Bu örnek için daha önce nasıl indiriceğimizi öğrendiğimiz, WDI veri setinden USA, Türkiye ve Japonya için kişi başı GSYH verilerini indirelim.
library(WDI)
gsyh <- WDI(country=c("US", "TR","JP"), indicator=c("NY.GDP.PCAP.CD"), start=1960, end=2020)
Veri setinin karışık isimlerini daha önce veri setini indirirken değiştirmiştik, bunu daha sonra da yapabilirsiniz.
names(gsyh) <- c("iso2c", "Ülke", "KisiBasiGSYH", "Sene")
head(gsyh)
## iso2c Ülke KisiBasiGSYH Sene
## 1 JP Japan 40193.25 2020
## 2 JP Japan 40777.61 2019
## 3 JP Japan 39808.17 2018
## 4 JP Japan 38891.09 2017
## 5 JP Japan 39400.74 2016
## 6 JP Japan 34960.64 2015
Serilerin grafiklerini gözlemleyelim, bu sefer plot fonksiyonu yerine ggplot paketini kullanalım.
library(ggplot2)
ggplot(gsyh, aes(Sene, KisiBasiGSYH, color=Ülke, linetype=Ülke)) + geom_line()
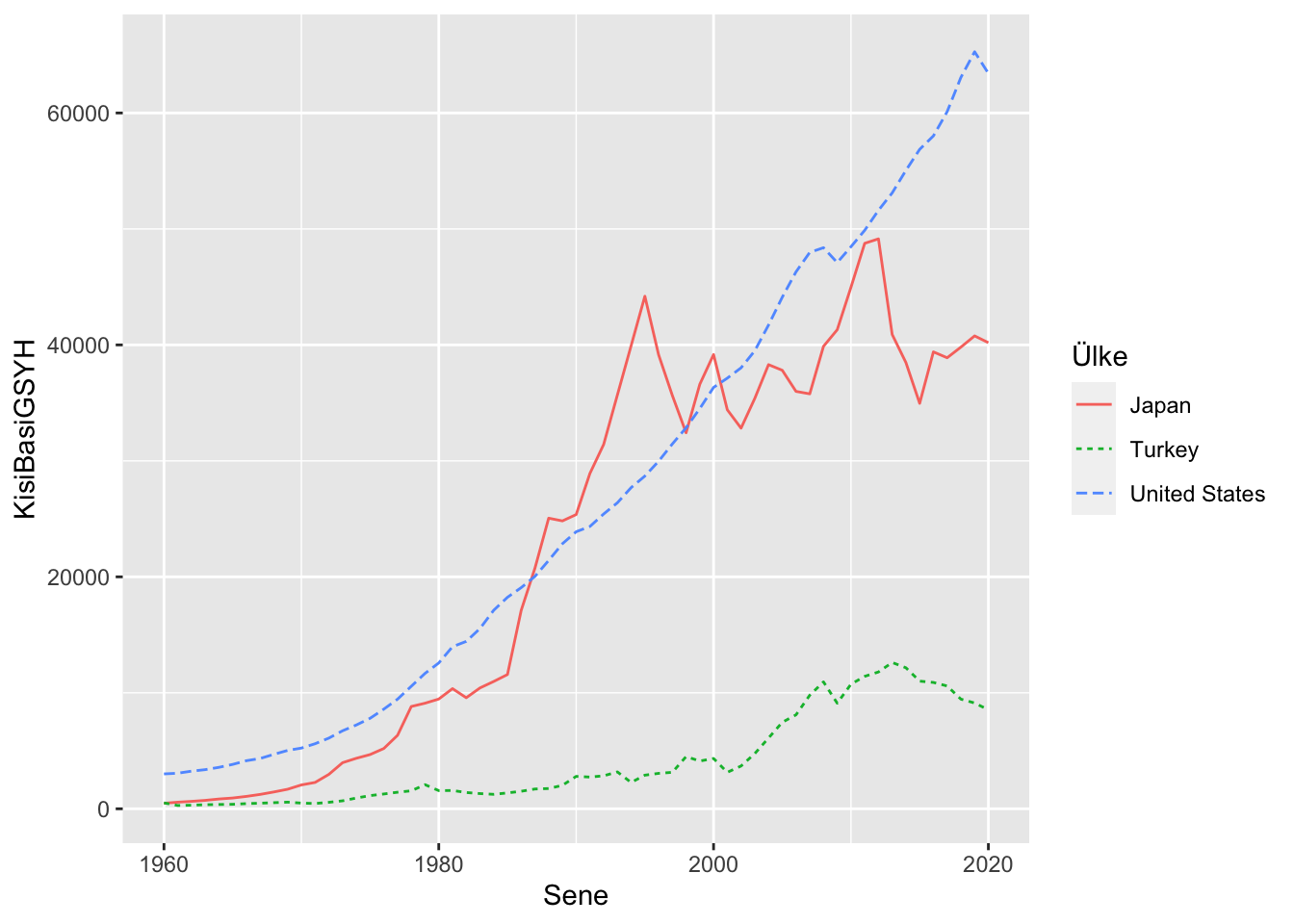
Bu veri seti üzerinden Türkiyenin veri setini ayıralım.
TR <- cbind(gsyh$KisiBasiGSYH[gsyh$Ülke == "Turkey"], gsyh$Sene[gsyh$Ülke == "Turkey"])
TR <- TR[order(TR[,2]),]
TR
## [,1] [,2]
## [1,] 509.4240 1960
## [2,] 283.8283 1961
## [3,] 309.4466 1962
## [4,] 350.6630 1963
## [5,] 369.5835 1964
## [6,] 386.3581 1965
## [7,] 444.5495 1966
## [8,] 481.6937 1967
## [9,] 526.2135 1968
## [10,] 571.6178 1969
## [11,] 489.9304 1970
## [12,] 455.1049 1971
## [13,] 558.4209 1972
## [14,] 686.4901 1973
## [15,] 927.7992 1974
## [16,] 1136.3756 1975
## [17,] 1275.9566 1976
## [18,] 1427.3718 1977
## [19,] 1549.6444 1978
## [20,] 2079.2203 1979
## [21,] 1564.2472 1980
## [22,] 1579.0738 1981
## [23,] 1402.4064 1982
## [24,] 1310.2557 1983
## [25,] 1246.8245 1984
## [26,] 1368.4017 1985
## [27,] 1510.6763 1986
## [28,] 1705.8944 1987
## [29,] 1745.3649 1988
## [30,] 2021.8595 1989
## [31,] 2794.3505 1990
## [32,] 2735.7076 1991
## [33,] 2842.3700 1992
## [34,] 3180.1876 1993
## [35,] 2270.3373 1994
## [36,] 2897.8666 1995
## [37,] 3053.9472 1996
## [38,] 3144.3857 1997
## [39,] 4499.7375 1998
## [40,] 4116.1706 1999
## [41,] 4337.4780 2000
## [42,] 3142.9210 2001
## [43,] 3687.9561 2002
## [44,] 4760.1040 2003
## [45,] 6101.6321 2004
## [46,] 7456.2961 2005
## [47,] 8101.8569 2006
## [48,] 9791.8825 2007
## [49,] 10941.1721 2008
## [50,] 9103.4741 2009
## [51,] 10742.7750 2010
## [52,] 11420.5555 2011
## [53,] 11795.6335 2012
## [54,] 12614.7816 2013
## [55,] 12157.9904 2014
## [56,] 11006.2795 2015
## [57,] 10894.6034 2016
## [58,] 10589.6677 2017
## [59,] 9454.3484 2018
## [60,] 9121.5152 2019
## [61,] 8536.4333 2020
TR verisetini daha önce anlatmış olduğumuz zaman serisi ts() fonksiyonunu kullanarak zaman serisi veri setine dönüştürelim. Ancak bu sefer sene’nin ne zaman başlayıp bittiğini bilmediğinizi varsayıyorum. Bu yüzden veri setinin başlangıç ve bitiş tarihlerini max ve min fonksiyonlarından yardım alarak yazalım.
TR <- ts(TR[,1], start=min(gsyh$Sene), end=max(gsyh$Sene))
Tabiki grafiğini göstermemiz lazım.
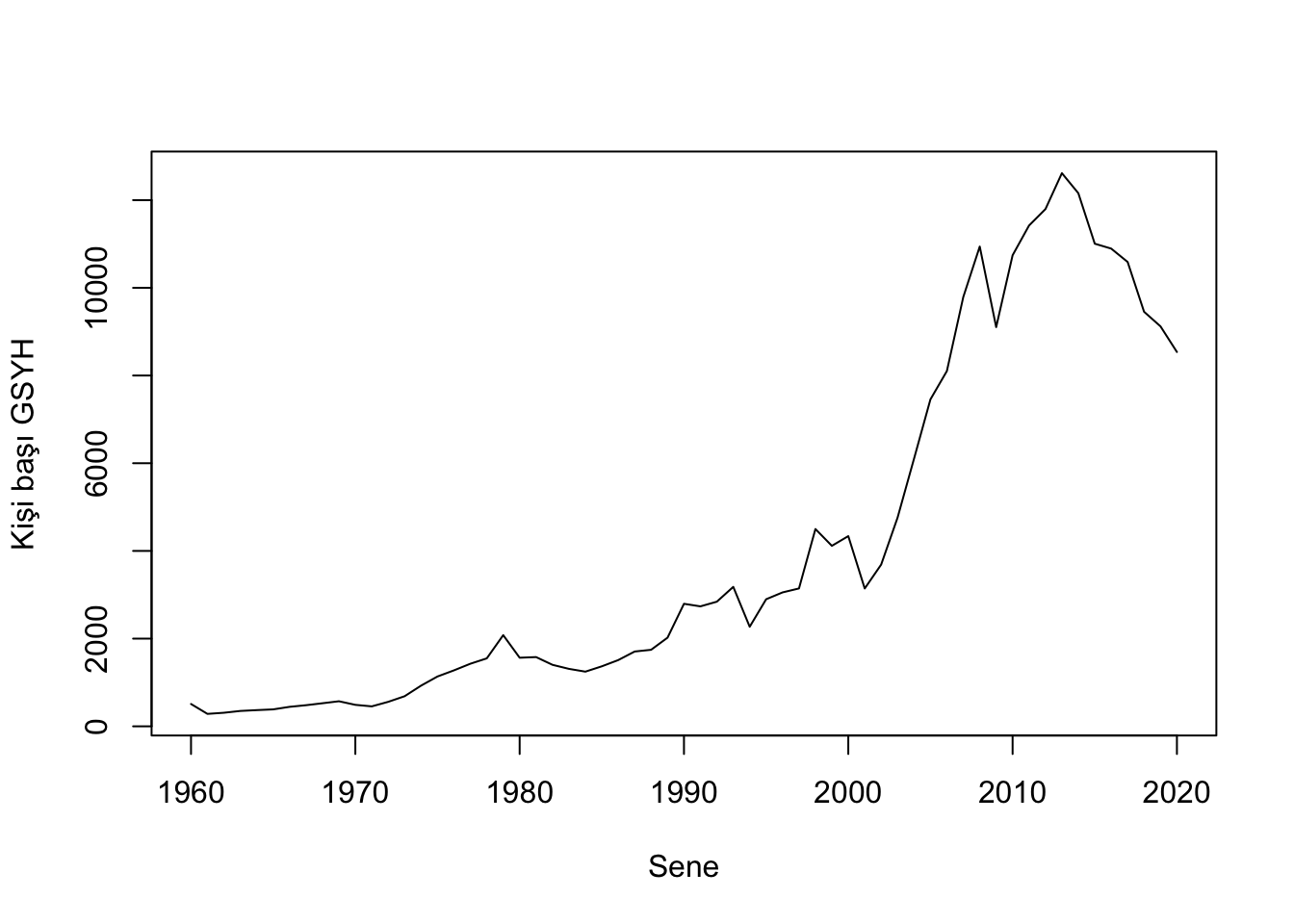
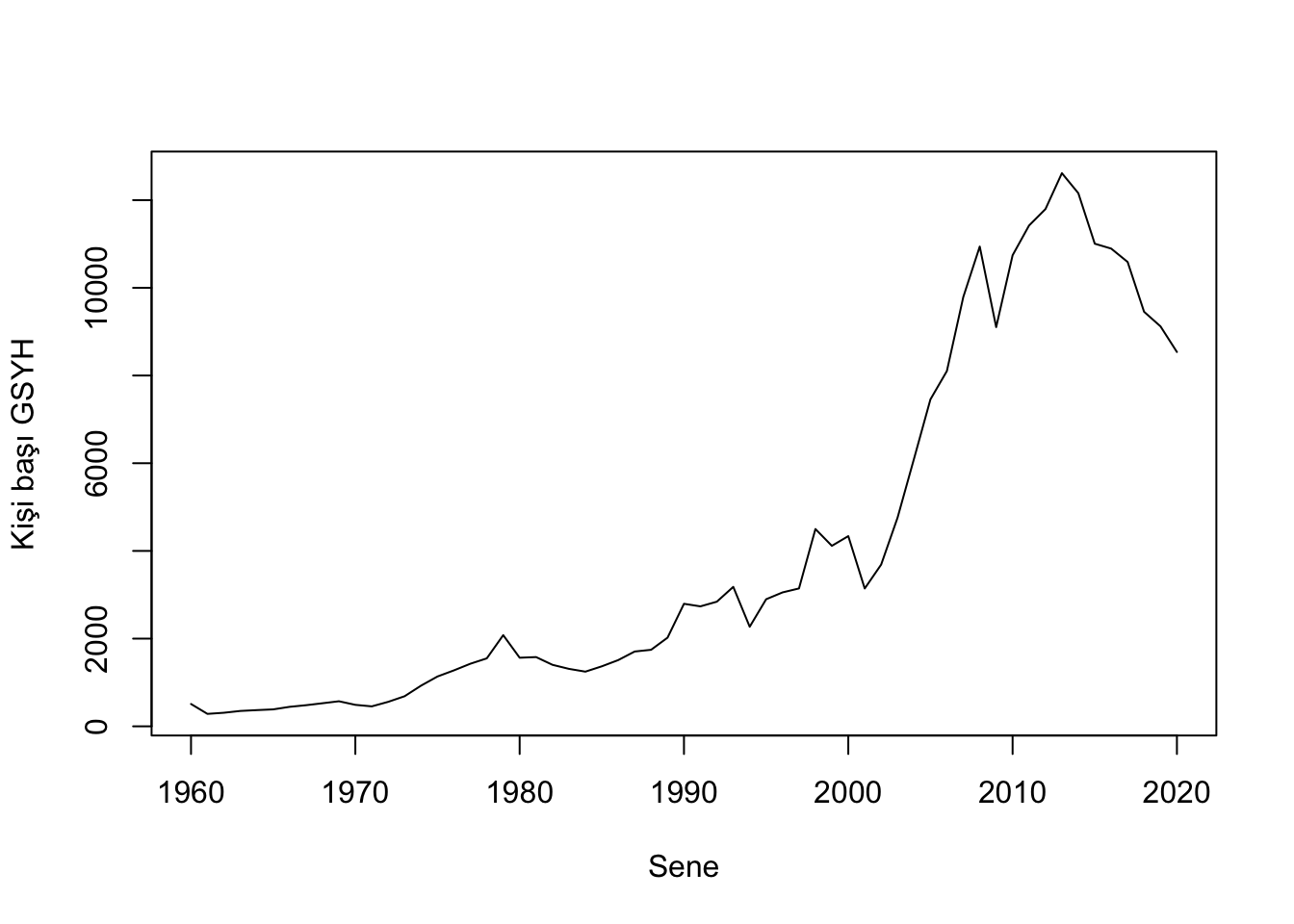
plot(TR, ylab="Kişi başı GSYH", xlab="Sene")
Şimdi tekrar geçen derslerde öğrendiğimiz, ACF (otokorelasyon) grafiğine bakalım. Bir de parçalı otokorelasyon (PACF) grafiğini açıklayalım.
acf(TR)
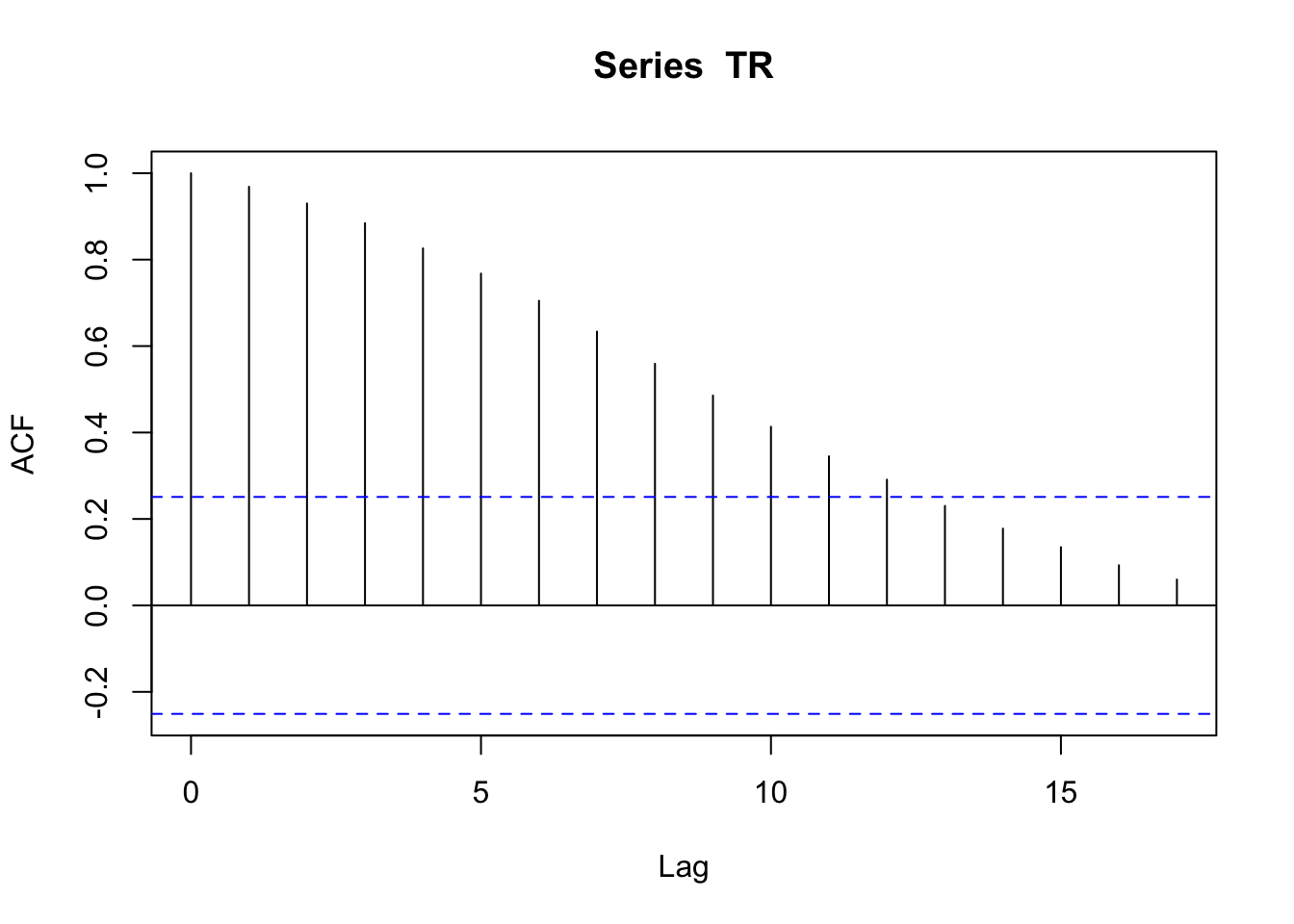
ACF grafiğine baktığımızda, kişi başı GSHY serisinin kendisinin gecikmeli serileriyle korelasyona sahip olduğunu görüyoruz. Kişi başı GSYH kendisinden bir önceki zaman dilimine çok bağımlı ve bu bağımlılık 12. gecikmeye kadar azalarak devam ediyor.
pacf(TR)
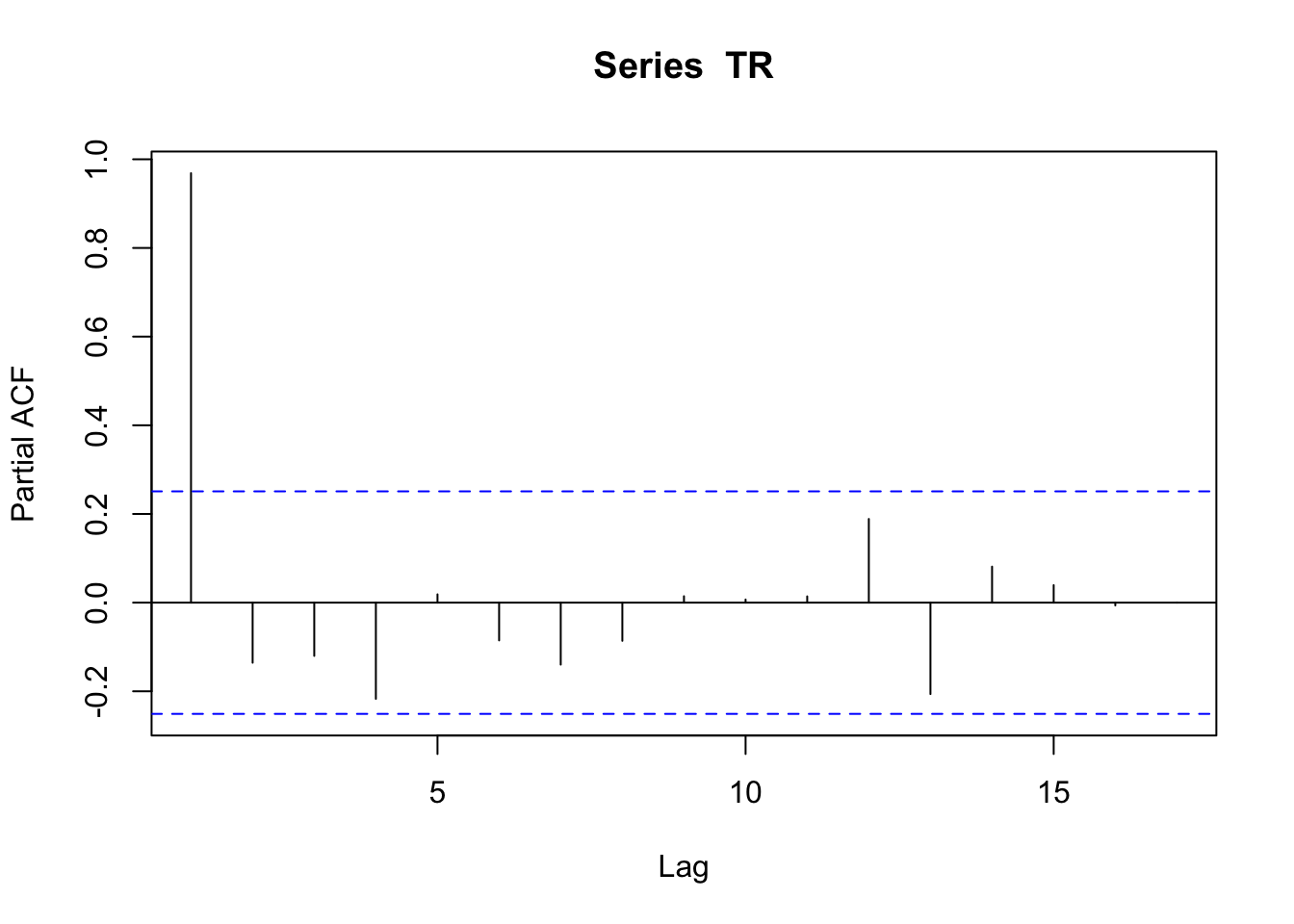Partial otokorelasyona baktığımızda aynı bağımlılığı gözlemlemiyoruz. Birinci gecikme çok büyük bir korelasyona sahip. Partial grafiği bize diğer zaman dilimlerinin bağımlılığın sadece kendilerinin birinci gecikmesi dolayısıyla kaynaklandığını ispatlıyor. Partial korelasyon sıradaki gecikmenin diğer gecikmelerden etkilenmeden zaman serisiyle ne kadar korelasyona sahip olduğunu gösterir. Bu grafikler zaman serisinin durağan olmadığının kanıtları gibidir. Zaten serinin grafiğine baktığınızda, durağan olmadığını serinin farklı zaman dilimlerinde bulunan ortalamalarından da anlayabilirsiniz.
plot(TR, ylab="Kişi başı GSYH", xlab="Sene")
Bu otokorelasyon ve partial otokorelasyon fonksiyonunu regresyon formunda gösterelim.
$$ y_t = \alpha_0 + \alpha_1 y_{t-1} + u $$
$alpha_1$ $y$‘nin birinci gecikmesiyle arasında olan otokorelasyonu gösteriyor. Bu regresyonu örneğimiz için yapalım ve $alpha$ katsayılarını gözlemleyelim.
library(dynlm)
## Loading required package: zoo
##
## Attaching package: 'zoo'
## The following objects are masked from 'package:base':
##
## as.Date, as.Date.numeric
Ilkgecikme <- dynlm(TR ~ L(TR, 1))
summary(Ilkgecikme)
##
## Time series regression with "ts" data:
## Start = 1961, End = 2020
##
## Call:
## dynlm(formula = TR ~ L(TR, 1))
##
## Residuals:
## Min 1Q Median 3Q Max
## -1903.5 -229.7 -58.7 223.2 1596.5
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 172.73437 122.19650 1.414 0.163
## L(TR, 1) 0.99022 0.02182 45.383 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 665.2 on 58 degrees of freedom
## Multiple R-squared: 0.9726, Adjusted R-squared: 0.9721
## F-statistic: 2060 on 1 and 58 DF, p-value: < 2.2e-16
İlk gecikme katsayısı 0.99 olarak görünüyor.
Ikincigecikme <- dynlm(TR ~ L(TR, 2))
summary(Ikincigecikme)
##
## Time series regression with "ts" data:
## Start = 1962, End = 2020
##
## Call:
## dynlm(formula = TR ~ L(TR, 2))
##
## Residuals:
## Min 1Q Median 3Q Max
## -1719.8 -492.9 -260.8 275.6 2637.7
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 363.85199 180.93530 2.011 0.0491 *
## L(TR, 2) 0.97998 0.03277 29.905 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 984.6 on 57 degrees of freedom
## Multiple R-squared: 0.9401, Adjusted R-squared: 0.939
## F-statistic: 894.3 on 1 and 57 DF, p-value: < 2.2e-16
Diğer gecikmeleri katmadan ikinci gecikme için yapılan regresyonda yine gecikmenin katsayısı 0.98 ve anlamlı.
Ucuncugecikme <- dynlm(TR ~ L(TR, 3))
summary(Ucuncugecikme)
##
## Time series regression with "ts" data:
## Start = 1963, End = 2020
##
## Call:
## dynlm(formula = TR ~ L(TR, 3))
##
## Residuals:
## Min 1Q Median 3Q Max
## -2281.4 -587.7 -239.6 450.4 3316.5
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 571.80137 234.78995 2.435 0.0181 *
## L(TR, 3) 0.96755 0.04325 22.371 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1277 on 56 degrees of freedom
## Multiple R-squared: 0.8994, Adjusted R-squared: 0.8976
## F-statistic: 500.4 on 1 and 56 DF, p-value: < 2.2e-16
Bu örnekler bu şekilde çoğaltılabilir. Katsayı hep bire yakın ve anlamlılık düzeyi çok yüksek.
Şimdi bu katsayıları birbirlerini kontrol ederek yazalım. İlk yazdığımız regresyon AR(1) olarak adlandırılıyor. Sadece bir gecikme ile yapılan regresyon.
$$ y_t = \alpha_0 + \alpha_1 y_{t-1} + u_t $$
Benzer bir regresyonu diğer gecikmeleri sabit tutarak katsayının anlamlığını ölçmek için AR(p) gecikmesine kadar yazabiliriz.
$$ y_t = \alpha_0 + \alpha_1 y_{t-1} + \alpha_2 y_{t-2} + \alpha_3 y_{t-3} + \alpha_4 y_{t-4} + … + \alpha_p y_{t-p} + u_t $$
Böyle bir regresyonu gecikme 10’a kadar yapalım, yani AR(10)
AR10 <- dynlm(TR ~ L(TR, c(1:10)))
summary(AR10)
##
## Time series regression with "ts" data:
## Start = 1970, End = 2020
##
## Call:
## dynlm(formula = TR ~ L(TR, c(1:10)))
##
## Residuals:
## Min 1Q Median 3Q Max
## -2124.75 -277.50 -56.73 337.91 1423.78
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 236.40345 158.63707 1.490 0.1440
## L(TR, c(1:10))1 1.03427 0.15747 6.568 7.53e-08 ***
## L(TR, c(1:10))2 0.06830 0.22724 0.301 0.7653
## L(TR, c(1:10))3 0.12906 0.22957 0.562 0.5771
## L(TR, c(1:10))4 -0.39876 0.23226 -1.717 0.0937 .
## L(TR, c(1:10))5 0.25626 0.24058 1.065 0.2932
## L(TR, c(1:10))6 0.01197 0.24336 0.049 0.9610
## L(TR, c(1:10))7 0.02645 0.23639 0.112 0.9115
## L(TR, c(1:10))8 -0.06448 0.24204 -0.266 0.7913
## L(TR, c(1:10))9 -0.02921 0.24118 -0.121 0.9042
## L(TR, c(1:10))10 -0.11036 0.19298 -0.572 0.5706
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 725 on 40 degrees of freedom
## Multiple R-squared: 0.9734, Adjusted R-squared: 0.9668
## F-statistic: 146.7 on 10 and 40 DF, p-value: < 2.2e-16
Farkındaysanız aynı partial otokorelasyon (pacf) grafiğinde gösterdiği gibi diğer gecikmeleri kontrol edince birtek ilk gecikme anlamlılık düzeyine sahip oluyor, ve katsayı 1’e çok yakın. Bu katsayının doğru olduğunu kabul edersek regresyon fonksiyonumuz şu şekilde yazılabilir.
$$ y_t = \alpha_0 + y_{t-1} + u_t $$ $\alpha_1$ 1’e eşit olduğu için katsayının yerine bir yazabildik. $y_{t-1}$‘i sol tarafa atarsak
$$ y_t - y_{t-1}= \alpha_0 + u_t $$ $$ \Delta y_t = \alpha_0 + u_t $$ olarak yazabiliriz.
Yani sabit bir sayı ve rastgele hata payı. O zaman eğer $\alpha_1$ 1’e eşit olan bir zaman serisinin farkını alırsak durağan bir seriye çevirebiliriz diyebiliriz.
$$ y_t = \alpha_0 + y_{t-1} + u_t $$ şeklinde yazılabilen serilere durağan olmayan (nonstationary) zaman serileri denir. Bu tür $\alpha_1$ 1’e eşit olan AR(1) süreci rastege yürüme (random walk) olarak bilinir.
Zaman serisi bir önceki bulunduğu konuma tamamen bağımlı ve üstüne rastgele bir hata alarak ilerlemesi olarak bilinirler.
Random Walk Örneği
İki random walk durağan olmayan seri yaratalım ve regresyona sokalım.
Serilerin 200 gözlemi olsun.
n<-200
hata payı rastgele olsun ve isimlerine $u$ ve $\v$ diyelim. $u$ ve $v$ hata payları rastgele ve normal dağılıma sahip olsun.
u <- ts(rnorm(n))
v <- ts(rnorm(n))
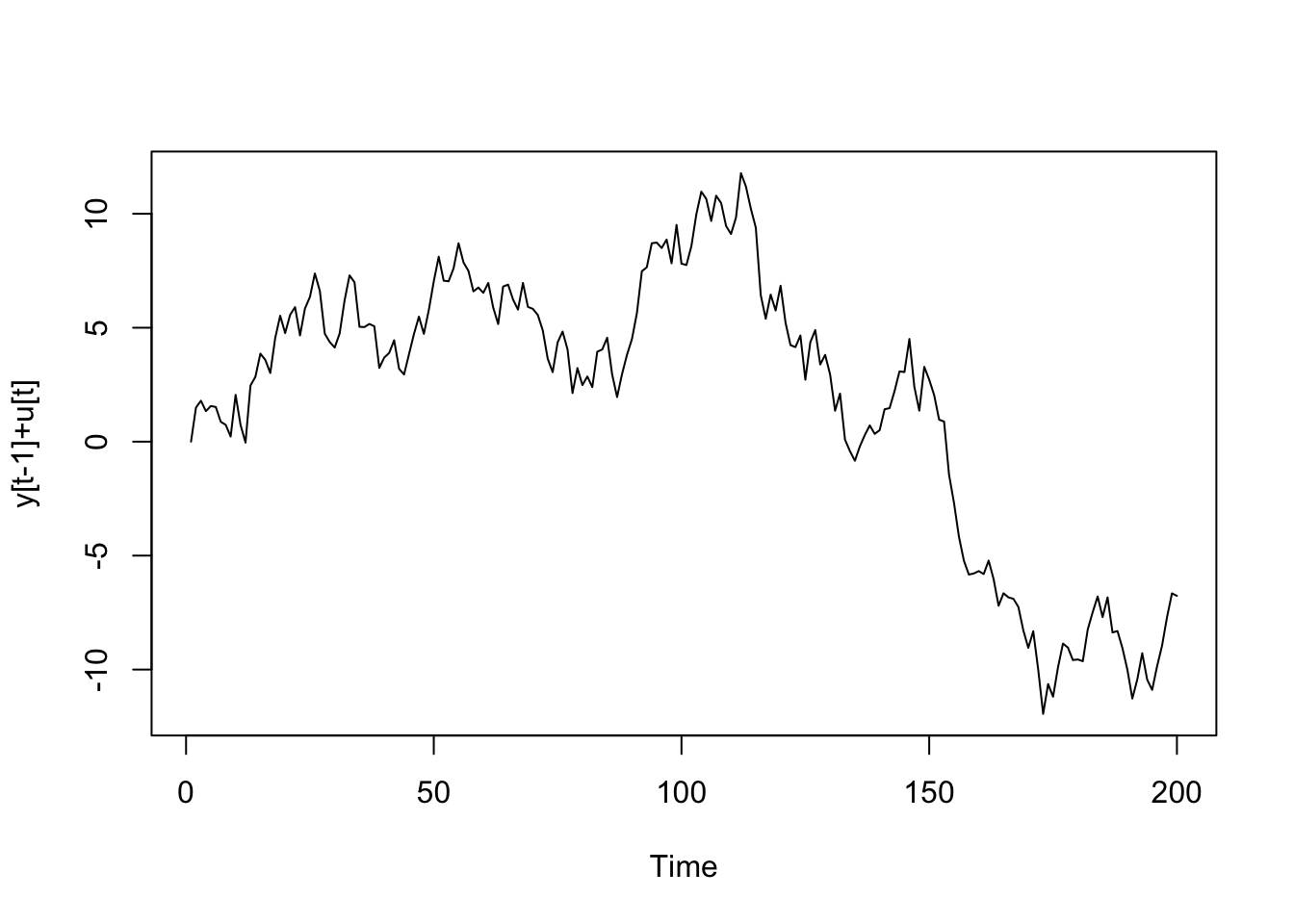
y ismini vereceğimiz zaman serisi random walk bir yapıya sahip olacak ve bir önceki gecikmesine u hata payı eklenerek bulunacak.
$$ y_t = \alpha_0 + y_{t-1} + u_t $$
y <- ts(rep(0,n))
for (t in 2:n){
y[t]<- y[t-1]+u[t]
}
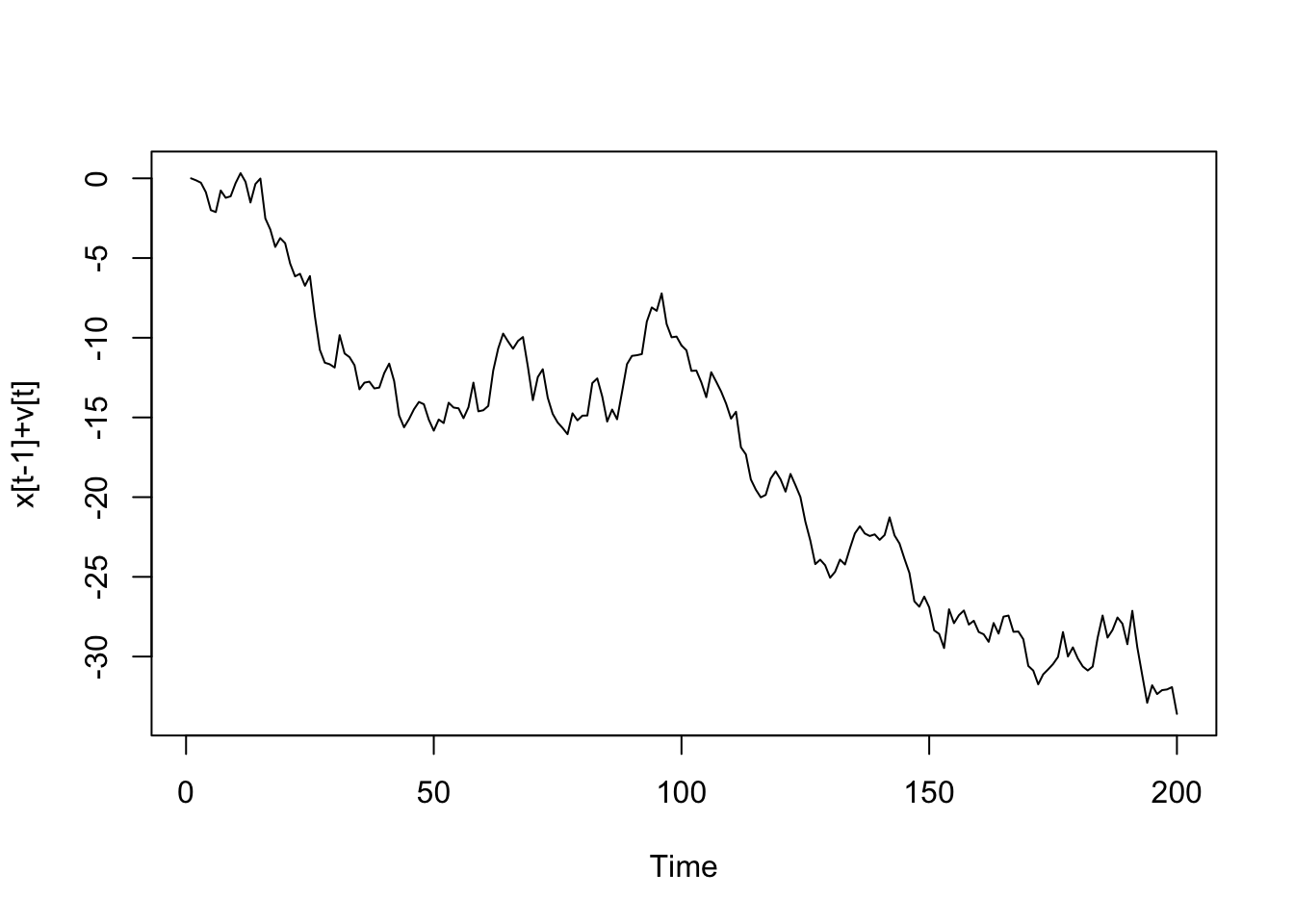
x zaman serisi de aynı şekilde v hata payı eklenerek bulunacak.
x <- ts(rep(0,n))
for (t in 2:n){
x[t]<- x[t-1]+v[t]
}
Oluşturduğumuz iki rastgele zaman serisinin grafiklerine bakalım.
plot(y,type='l', ylab="y[t-1]+u[t]")
plot(x,type='l', ylab="x[t-1]+v[t]")
Şimdi bu iki rastgele oluşturulmuş zaman serisini regresyona sokalım. Tahmin edeceğiniz gibi bu iki serinin birbirleriyle bir ilişkisi yoktur ve regresyon sonucunun anlamsız çıkması beklenir. Ancak bu seriler random walk bir sürece sahip olduklarından ilişki anlamlı çıkacaktır. Sahte (spurious) regresyon örneğimiz
Spurious <- lm(y~x)
summary(Spurious)
##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.8872 -3.3523 0.5684 3.1598 9.6831
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.8872 0.6710 14.73 <2e-16 ***
## x 0.4616 0.0341 13.54 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.392 on 198 degrees of freedom
## Multiple R-squared: 0.4807, Adjusted R-squared: 0.4781
## F-statistic: 183.3 on 1 and 198 DF, p-value: < 2.2e-16
İki zaman serisini regresyona sokabilmek ve gerçekten torumlayabileceğimiz bir regresyon sonucu elde edebilmek için, zaman serilerini durağan hale getirmemiz gerekir. Serilerin deltasını almak bu yöntemlerden biriydi.
duragan <- dynlm(d(y) ~ d(x))
summary(duragan)
##
## Time series regression with "ts" data:
## Start = 2, End = 200
##
## Call:
## dynlm(formula = d(y) ~ d(x))
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.93065 -0.74576 -0.03907 0.83570 2.52706
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.03583 0.07298 -0.491 0.624
## d(x) -0.01083 0.07184 -0.151 0.880
##
## Residual standard error: 1.015 on 197 degrees of freedom
## Multiple R-squared: 0.0001153, Adjusted R-squared: -0.00496
## F-statistic: 0.02272 on 1 and 197 DF, p-value: 0.8803
Görüldüğü gibi hiçbir katsayı anlamlı değil. Bu daha önce yapmış olduğumuz regresyonun anlamsız olduğunun ispatıdır. Spurious regresyon normal hayatta çok sık karşımıza çıkar. Eğer durağan olmayan serileri regresyona sokarsanız, gerçekte olmayan ilişkiler bulabilirsiniz. Burada önemli olan durum durağanlığın test edilmesidir.
Durağanlık testi (Dickey Fuller)
Sizinde şimdiye kadar anlayacağınız üzere durağanlık testinde aslında $\alpha_1 = 1$ olup olmadığını test ediyouruz. Eğer bu hipotezimizi reddedemezsek, serinin durağan olmadığını düşünmek zorunda kalabiliriz. $y_{t-1}$‘i, $\alpha_1$‘i bir olarak kabul ettiğimizden eşitliğin sol tarafına atabiliriz. Varsayımımız doğruysa, ve eğer sağ tarafa tekrar $y_{t-1}$ eklersek bu sefer katsayısının 0 olmasını bekleyebiliriz.
$$ \Delta y_t = \beta_0 + \beta_1 y_{t-1} + u_t $$
$H_0: \beta_1 = 0$ Dickey Fuller testinin hipotezi olacaktır. Eğer $\beta_1 = 0$ olduğunu ispatlarsak, zaman serisinin durağan olamayabileceğini söyleyebiliriz. Burada kritik değerlerde bir değişiklik olacaktır. Artık regresyon için kullandığımız kritik değerleri kullanamayız. Kritik değerler, üç farklı değer alabilir. Sabiti ve trendi olmayan (no constant and no trend), sabiti olan trendi olmayan (constant and no trend), ve sabiti ve trendi olan (constant and trend)ç
Şimdi üç seri içinde durağanlık testini yapalım. Zaten iki seriyi, biz kendimiz random walk süreciyle yarattığımız için sonucu önceden biliyoruz.
library(tseries)
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoo
adf.test(x)
##
## Augmented Dickey-Fuller Test
##
## data: x
## Dickey-Fuller = -2.3233, Lag order = 5, p-value = 0.4407
## alternative hypothesis: stationary
Olasılık değeri (p-value) 0.86 olarak bulduk. Bunu $\beta_1$ değerinin sıfır olma olasılığı olarak da adlandırabilirsiniz. Sonuç olarak hipotezimizi reddedemedik ve serimiz durağan değildir.
adf.test(y)
##
## Augmented Dickey-Fuller Test
##
## data: y
## Dickey-Fuller = -2.0899, Lag order = 5, p-value = 0.5385
## alternative hypothesis: stationary
y zaman serisi için de beklediğimiz gibi seri durağan değil.
adf.test(TR)
##
## Augmented Dickey-Fuller Test
##
## data: TR
## Dickey-Fuller = -2.316, Lag order = 3, p-value = 0.447
## alternative hypothesis: stationary
Gördüğünüz gibi Türkiye’nin kişi başı GSYH verisi de durağan değil. Bunu daha önce acf ve pacf grafiklerine bakarak da anlamıştık.
Bir diğer durağanlık testi, hipotezin durağan olduğunu öne süren kpss testidir. Bu durumda olasılık değeri (p-value) küçükse hipotezimizi reddetmemiz gerekir.
kpss.test(TR)
## Warning in kpss.test(TR): p-value smaller than printed p-value
##
## KPSS Test for Level Stationarity
##
## data: TR
## KPSS Level = 1.348, Truncation lag parameter = 3, p-value = 0.01
Görüyoruz ki bu test de Dickey Fuller testi gibi, zaman serisinin durağan olmadığını söyler.
İlk farkı aldığımızda seri durağanlaşır mı?
Zaman serisinin ilk farkını alalım ve test yapalım.
Deltax <- diff(x)
adf.test(Deltax)
## Warning in adf.test(Deltax): p-value smaller than printed p-value
##
## Augmented Dickey-Fuller Test
##
## data: Deltax
## Dickey-Fuller = -5.4943, Lag order = 5, p-value = 0.01
## alternative hypothesis: stationary
Gördüğünüz üzere serinin ik farkını almak genellikle seriyi durağan hale getirir. Artık olasılık değeri 0.01 ve $\beta_1$ değerinin sıfır olma ihtimali çok düşük hale gelir.