R ile Çoklu Regresyon Analizi: Çıkarım: (Wooldridge Örnekleri)
Bu bölümde, çoklu regresyon analizine devam ediyoruz.
Popülasyon regresyon modelindeki parametrelerle ilgili hipotezleri test etmemiz gerekiyor. En küçük kareler yöntemiyle tahmin ettiğimiz parametrelerin dağılımlarına bakacağız ve normal dağılıp dağılmadığını anlamaya çalışacağız. Daha sonra parametrelerle ilgili hipotez testlerini oluşturacağız.
En küçük kareler tahmincilerinin örneklem dağılımları
Bu bölüme başlamadan önce 6. varsayımımızı hatırlamamız gerekecek.
- Altıncı Varsayım (MLR.6): Normalite (Normality), popülasyon hatası $u$ açıklayıcı değişkenler, $x_1, x_2, …, x_k$, den bağımsızdır ve ortalaması sıfır, varyansı $\delta^2$ olmak üzere normal dağılmıştır. ($u \sim Normal(0,\delta^2)$)
Eğer MLR.6 varsayımını kabul etmek, MLR.4 ve MLR.5 varsayımlarını kabul etmemizi zorunlu kılar. MLR.1’den MLR.6’ya kadar olab varsayımlar klasik lineer model (CLM) varsayımları olarak bilinir. Klasik lineer model (CLM) varsayımları bütün Gauss-Markov varsayımları artı normal dağılan hatalar varsayımı olarak da bilinir.
Klasik lineer model (CLM) varsayımları sağlandığında en küçük kareler (OLS) yöntemi en az varyansa sahip ve sapmasız tahminci olarak adlandırılabilir. Unutulmamalıdır ki, bu varsayım çok güçlü bir varsayımdır ve sağlanması oldukça zordur. Örneğin maaşlar böyle bir değişkendir. Popülasyonda bulunan bir çok kişi minimum ücret alır ve maaşların sıfırın altına düşmesi söz konusu değildir. Gelir eşitsizliğine de bakarsak, maaşlar sağ kuyruğa doğru da oldukça uzayabilir.
Tek Bir Popülasyon Parametresi Hakkında Hipotezlerin Test Edilmesi: t Testi
Çoklu popülasyon modelimizi hatırlayalım
$$ y= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + … + \beta_k x_k + u $$
Bu bölümde herhangi bir $\beta_j$ parametresini test etmeyi öğreneceğiz.
CLM varsayımları sayesinde biliyoruz ki $\frac{\hat{\beta_j}-\beta_j}{se(\hat{\beta_j})} \sim Normal(0,1)$. Popülasyon için kullandığımız bu normal dağılım, örneklem için t-dağılımına dönüşür $\frac{\hat{\beta_j}-\beta_j}{se(\hat{\beta_j})} \sim t_{n-k-1}=t_{df}$. n-k-1 t-dağılımının esneklik derecesini (degrees of freedom, df) verir. n veri setinde kaç gözlem olduğunu, k modelimizde kaç bağımsız değişken olduğunu söyler.
Bir örnek vermemiz gerekirse maaş veri seti üzerinden tartışabiliriz.
$$ maaş= \beta_0 + \beta_1 eğitim + \beta_2 deneyim + \beta_3 iş.yılı + u $$
Bir hipotez kurup test etmek istediğimizde, katsayılardan birini seçip $H_0$ nul hipotezini kurabiliriz.
Örneğin,
$H_0: \beta_2=0$, eğitim ve iş yılı sabit tutulduğunda, deneyimin saatlik maaşlar üzerinde hiçbir etkisi yoktur anlamı taşır. Eğer bu hipotez doğruysa, şu anda çalışdığı işten önce kişinin çalışmış olduğu yılların ücretin üzerinde hiçbir etkisi olmadığı anlamı çıkar. Eğer $\beta_2>0$ ise, önceki iş yılları, üretkenliğe dolayısıyla ücretlere pozitif etki yapmaktadır.
$H_0: \beta_2=0$ olup olmadığını test ettiğimize göre, t istatistiğini (t oranı) şu şekide bulabiliriz.
$t_{\hat{\beta_j}} = \frac{\hat{\beta_j}}{se(\hat{\beta_j})}$
$\beta_2$‘nun sıfır olup olmadığını ($\beta_2 \neq 0$) test etmek için $t_{\hat{\beta_j}}$ iyi bir araç mı? $H_0: \beta_2=0$ test ediyoruz, fakat gerçek $\beta_2$ değerini bilmiyoruz. Ancak elimizde $\beta_2$ değerinin en iyi sapmasız tahmini $\hat{\beta_j}$ var. $H_0: \beta_2=0$ gerçek olsa bile, biz asla bu gerçek değere sahip olan bir $\hat{\beta_j}$ değerine sahip olamıyacağız. Asıl sormamız gereken soru, tahminimiz $\hat{\beta_j}$‘nin sıfıra ne kadar yakın olduğu. Bu ölçünün uzaklığını bize ancak standart hata değeri verebilir. Standar hata sayesinde $\hat{\beta_j}$ değerinin sıfırdan kaç standart sapma uzak olduğunu hesaplayabiliriz. Bu kaç standart sapma uzaklıkta oldğunu veren değer $t_{\hat{\beta_j}}$ değeridir. $t_{\hat{\beta_j}}$ değeri ne kadar büyükse, gerçek parametre değerimiz sıfırdan o kadar uzaktır ve $H_0: \beta_2=0$ hipotezini reddetmemiz için o kadar kanıt sağlar.
Örnek 4.1 Saatlik Maaş Denklemi
Wooldridge wage1 datasını kullanalım.
library(wooldridge)
data(wage1)
Verilere bir göz gezdirin.
head(wage1)
## wage educ exper tenure nonwhite female married numdep smsa northcen south
## 1 3.10 11 2 0 0 1 0 2 1 0 0
## 2 3.24 12 22 2 0 1 1 3 1 0 0
## 3 3.00 11 2 0 0 0 0 2 0 0 0
## 4 6.00 8 44 28 0 0 1 0 1 0 0
## 5 5.30 12 7 2 0 0 1 1 0 0 0
## 6 8.75 16 9 8 0 0 1 0 1 0 0
## west construc ndurman trcommpu trade services profserv profocc clerocc
## 1 1 0 0 0 0 0 0 0 0
## 2 1 0 0 0 0 1 0 0 0
## 3 1 0 0 0 1 0 0 0 0
## 4 1 0 0 0 0 0 0 0 1
## 5 1 0 0 0 0 0 0 0 0
## 6 1 0 0 0 0 0 1 1 0
## servocc lwage expersq tenursq
## 1 0 1.131402 4 0
## 2 1 1.175573 484 4
## 3 0 1.098612 4 0
## 4 0 1.791759 1936 784
## 5 0 1.667707 49 4
## 6 0 2.169054 81 64
Kullanacağımız değişkenlerin açıklamalarına bakalım.
?wage1
Kullanacağımız değişkenlerin açıklamalarını daha önce çevirdik. İsterseniz help(wage1) veya ?wage1 kodlarını kullanarak veriler hakkında bilgiye ulaşabilirsiniz.
Bu veri setini kullanarak deneyimin getirisini test etmeye çalışacağız, bunu yaparken eğitim ve güncel işindeki çalışma yıllarını kontrol edeceğiz.
$$ log(maaş)= \beta_0 + \beta_1 eğitim + \beta_2 deneyim + \beta_3 iş.yılı + u $$ veri setindeki ingilizce değişkenler
$$ log(wage)= \beta_0 + \beta_1 educ + \beta_2 exper + \beta_3 tenure + u $$
Diğer iki değişkeni sabit tutarken, deneyimin getirisinin sıfır olup olmadığını test etmek için kurduğumuz hipotez $H_0: \beta_2=0$ olaarak yazılabilir. Bu hipotezi reddersek $H_1: \beta_2>0$ alternatif hipotezini kabul ediyoruz.
maasreg <- lm(log(wage)~ educ+exper+tenure,data = wage1)
summary(maasreg)
##
## Call:
## lm(formula = log(wage) ~ educ + exper + tenure, data = wage1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.05802 -0.29645 -0.03265 0.28788 1.42809
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.284360 0.104190 2.729 0.00656 **
## educ 0.092029 0.007330 12.555 < 2e-16 ***
## exper 0.004121 0.001723 2.391 0.01714 *
## tenure 0.022067 0.003094 7.133 3.29e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4409 on 522 degrees of freedom
## Multiple R-squared: 0.316, Adjusted R-squared: 0.3121
## F-statistic: 80.39 on 3 and 522 DF, p-value: < 2.2e-16
$\beta_2$‘nun popülasyon parametresi olduğunu unutmayın. Biz popülasyon parametresini test ediyoruz. exper’in tahmini katsayısı $\hat{\beta_2}$ gördüğünüz gibi 0.0041. Hipotezi tekrar yazmak isterseniz $0.0041=0$ ya da $H_0:\hat{\beta_2}=0$ yazamazsınız.
Veri setimizde her bir değişken için gözlem sayısı $n=526$, t dağılımı için serbestlik derecesini bulmak isterseniz $n-k-1= 526-3-1=522$ değerini kullanmanız gerekecektir. Bu değer aslında regresyon sonuçlarında “degrees of freedom” değeri olarak yazıldığına dikkat edin (Alttan üçüncü satır “Residual standard error: 0.4409 on $\bf{522}$ $\bf{degrees}$ $\bf{of}$ $\bf{freedom}$”.
R-studio ile 522 serbestlik derecesine sahip t dağılımının kritik değerlerini bulmak çok kolaydır. Bunun için bir formüle ya da tabloya ihtiyacımız yok. qt komutu size bu değeri verecektir.
Mesela eğer %95 olasılıkta t değerini bulmak istiyorsanız aşağıdaki kod yeterli olacaktır.
qt(0.95,522)
## [1] 1.647778
%99 olasılıkta t değeri için
qt(0.99,522)
## [1] 2.333513
kullanıyoruz. 522 gibi büyük bir gözlem sayısına sahip olduğumuz için t değerlerimiz, normal dağılım kritik değerlerine çok yakındır. Kritik t değerini bulduktan sonra, regresyon tablomuzda karşılaştırma yapmak istediğimiz parametrenin t değerine bakalım. Exper değişkeni için bu değer t value’nun altında 2.391 olarak bulunur. 2.39 iki kritik değerimizden de büyük bu durumda $\hat{\beta_{exper}}$ veya exper %1 seviyesinde istatistiksel olarak anlamlıdır ve %1 anlamlılık seviyesinde istatiksel olarak sıfırdan büyüktür. Unutmayın ki negatif bir t değerini kritik değerlerle karşılaştırıyor olabilirdik. Böyle bir durumda t değerinin mutlak değerinin kritik t değerlerinden büyük olup olmadığına bakacaktık.
Aynı cevabı t değerlerine bakmadan olasılıklara bakarak da çıkarabilirdik. Tekrar regresyon tablomuza bir göz atın. Her bir değişken için olasılık değerlerini Pr (probability, olasılık) sütununda göreceksiniz. Biz exper değişkeni için olasılık değerine bakıyoruz. Olasılık 0.01714, exper katsayısının sıfır olma olasılığını yaklaşık olarak %1.7 versede, biz t değerine göre %1’in altında bulmuştuk. Bu durum kafanızı karıştırmamalı. Çünkü R p değerini her zaman iki taraflı test olarak verecektir. Eğer 0.01714 değerini 2’ye bölersek 0.00857 buluruz. Gördüğünüz gibi exper katsayısının 0 olma ihtimali %1’den küçüktür. Bu yüzden $H_0$ hipotezini reddederiz.
Güven Aralığı
Güven aralığını oluşturmayı daha önce basit bir konsepte konuşmuştuk. Örneğin bir parametre için %95 güven aralığı oluşturmak istiyorsak, bulduğumuz katsayı sonucunun standart hatasının iki katından çıkarıyor ve topluyorduk.
$$ \beta_j \pm 2 \cdot se(\beta_j) $$
Burada 2 yerine hangi yüzdeyle güven aralığı oluşturmak isteniyorsa o t kritik değeri kullanılmalıdır.
R bizim için bu güven aralıklarını kolaylıkla oluşturabilir. Örneğimizden devam edecek olursak
confint(maasreg)
## 2.5 % 97.5 %
## (Intercept) 0.0796755842 0.48904353
## educ 0.0776292137 0.10642876
## exper 0.0007356983 0.00750652
## tenure 0.0159896850 0.02814475
confint bizim için %95 güven aralığını oluşturacaktır. %99 güven aralığı oluşturmak isterseniz
confint(maasreg, level=0.99)
## 0.5 % 99.5 %
## (Intercept) 0.0149982043 0.553720906
## educ 0.0730790792 0.110978894
## exper -0.0003340459 0.008576264
## tenure 0.0140692666 0.030065168
level detayını eklemeniz gerecektir.
Coefplot paketini yüklerseniz size güven aralığı grafiğini çıkaran bir kod sunar.
library(ggplot2)
library(coefplot)
coefplot(maasreg)
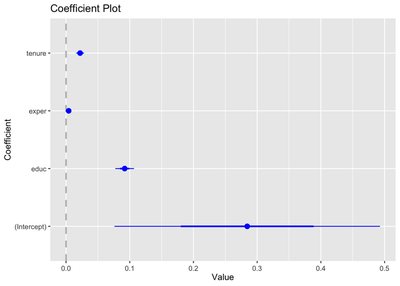
Grafikten de görebileceğiniz gibi exper katsayısı 0’a çok yakın ama güven aralığı 0’ı kapsamıyor.
Çoklu Doğrusal Kısıtların Testi
Şimdiye kadar sadece bir parametrenin testi üzerinde durduk ve hipotezi bir katsayının sıfıra eşit olup olmadığı üzerinden kurduk. Ancak bir kaç değişkenin katsayısının aynı anda test edilmesi de mümkündür. Beş değişkenli bir model düşünün
$$ y= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + \beta_4 x_4 + \beta_5 x_5 + u $$ $\beta_3, \beta_4, \beta_5$ katsayılarını aynı anda sıfır olup olmadığını merak ediyorsanız hipotezinizi şöyle oluşturursunuz
$$ H_0: \beta_3=0, \beta_4=0, \beta_5=0 $$
Farkındaysanız eğer bu hipotezi kabul edersek kısıtlı bir model elde etmiş oluruz.
$$ y= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + u $$
Bu iki model arasında hangi modelin doğru olduğunu F istatistiği ile kontrol ederiz. İlk modelimize kısıtsız model (unrestricted model, ur), ikinci modele ise kısıtlı model (restricted, r) diyeceğiz. F istatistiği şu şekide bulunur.
$$ F= \frac{(SSR_r-SSR_{ur})/q}{SSR_{ur}/(n-k-1)} $$ $SSR_r$ kısıtlı modelin hata payının karelerinin toplamı, $SSR_{ur}$ kısıtsız modelin hata payının karelerinin toplamı, $q$ kısıt sayısı, $n-k-1$ kısıtsız modelin serbestlik derecesidir. F testi yaparken de t testi yaptığımızdabulduğumuz gibi bir F kritik değeri bulmamız gerekli. Ancak bu sefer t tablo değeri değil, F tablo değeri kullanmalıyız. Bulmamız gereken F değeri $F_{q, n-k-1}$ değeridir. F dağılımı için %10, %5, %1’lik kritik değerler mevcuttur.
F istatistiğini bulmanın bir başka yolu $R^2$ kullanmaktır.
$$ F= \frac{R^2_{ur}-R^2_r}{1-R^2_{ur}} \cdot \frac{n-k-1}{q} $$
Dışlama Kısıtlarının Test Edilmesi Örneği
F testi örneği için kullanacağımız data seti HPRICE1. Şimdi bu veri setini yükleyelim ve verilere bir göz atalım.